Question Number 175806 by Ml last updated on 07/Sep/22
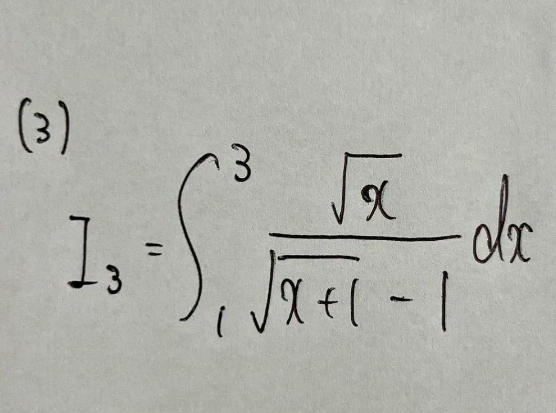
Answered by cortano1 last updated on 07/Sep/22
![((√x)/( (√(x+1))−1)) = (((√x) ((√(x+1)) +1))/x) = (((√(x+1)) +1)/( (√x))) let (√x) =tan u⇒x=tan^2 (u) { ((x=1⇒u=(π/4))),((x=3⇒u=(π/3))) :} I_3 = ∫_(π/4) ^(π/3) (((√(tan^2 (u)+1)) +1)/(tan u)) (2 tan u sec^2 u)du I_3 =∫_(π/4) ^(π/3) (sec u+1)(2sec^2 u)du I_3 =2∫_(π/4) ^(π/3) sec^3 u du+2[ tan u ]_(π/4) ^(π/3) I_3 =2((√3)−1)+2∫_(π/4) ^(π/3) sec u d(tan u) Ω = ∫sec u d(tan u)=sec u tan u−∫sec u(sec^2 u−1)du Ω=sec u tan u−Ω+∫sec u du Ω=(1/2)sec u tan u+((ln ∣sec u+tan u∣)/2) + c I_3 =2(√3)−2 +2.(1/2) [ sec u tan u+ln ∣sec u+tan u∣ ]_(π/4) ^(π/3) I_3 =2(√3)−2+2(√3) +ln (2+(√3))−(√2)−ln (1+(√2)) I_3 =4(√3)−2−(√2)+ln (((2+(√3))/( (√2)+1))) I_3 =4(√3)−2−(√2)+ln ((2+(√3))((√2)−1)) I_3 =4(√3)−2−(√2) +ln (2(√2)−2+(√6)−(√3))](https://www.tinkutara.com/question/Q175813.png)
$$\:\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{1}}\:=\:\frac{\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{x}+\mathrm{1}}\:+\mathrm{1}\right)}{\mathrm{x}} \\ $$$$\:=\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}\:+\mathrm{1}}{\:\sqrt{\mathrm{x}}}\: \\ $$$$\:\mathrm{let}\:\sqrt{\mathrm{x}}\:=\mathrm{tan}\:\mathrm{u}\Rightarrow\mathrm{x}=\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{u}\right) \\ $$$$\:\begin{cases}{\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{u}=\frac{\pi}{\mathrm{4}}}\\{\mathrm{x}=\mathrm{3}\Rightarrow\mathrm{u}=\frac{\pi}{\mathrm{3}}}\end{cases} \\ $$$$\:\mathrm{I}_{\mathrm{3}} =\:\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\:\frac{\sqrt{\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{u}\right)+\mathrm{1}}\:+\mathrm{1}}{\mathrm{tan}\:\mathrm{u}}\:\left(\mathrm{2}\:\mathrm{tan}\:\mathrm{u}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\right)\mathrm{du} \\ $$$$\:\mathrm{I}_{\mathrm{3}} =\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\:\left(\mathrm{sec}\:\mathrm{u}+\mathrm{1}\right)\left(\mathrm{2sec}\:^{\mathrm{2}} \mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{2}\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\mathrm{sec}\:^{\mathrm{3}} \mathrm{u}\:\mathrm{du}+\mathrm{2}\left[\:\mathrm{tan}\:\mathrm{u}\:\right]_{\pi/\mathrm{4}} ^{\pi/\mathrm{3}} \\ $$$$\:\mathrm{I}_{\mathrm{3}} =\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)+\mathrm{2}\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\mathrm{sec}\:\mathrm{u}\:\mathrm{d}\left(\mathrm{tan}\:\mathrm{u}\right) \\ $$$$\:\Omega\:=\:\int\mathrm{sec}\:\mathrm{u}\:\mathrm{d}\left(\mathrm{tan}\:\mathrm{u}\right)=\mathrm{sec}\:\mathrm{u}\:\mathrm{tan}\:\mathrm{u}−\int\mathrm{sec}\:\mathrm{u}\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}−\mathrm{1}\right)\mathrm{du} \\ $$$$\Omega=\mathrm{sec}\:\mathrm{u}\:\mathrm{tan}\:\mathrm{u}−\Omega+\int\mathrm{sec}\:\mathrm{u}\:\mathrm{du} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{u}\:\mathrm{tan}\:\mathrm{u}+\frac{\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{u}+\mathrm{tan}\:\mathrm{u}\mid}{\mathrm{2}}\:+\:\mathrm{c} \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\:+\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\mathrm{sec}\:\mathrm{u}\:\mathrm{tan}\:\mathrm{u}+\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{u}+\mathrm{tan}\:\mathrm{u}\mid\:\right]_{\pi/\mathrm{4}} ^{\pi/\mathrm{3}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\:+\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)−\sqrt{\mathrm{2}}−\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}−\sqrt{\mathrm{2}}+\mathrm{ln}\:\left(\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right) \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}−\sqrt{\mathrm{2}}+\mathrm{ln}\:\left(\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right) \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}−\sqrt{\mathrm{2}}\:+\mathrm{ln}\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}+\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}\right) \\ $$
