Question Number 175814 by Mortalis last updated on 07/Sep/22

Commented by Mortalis last updated on 07/Sep/22
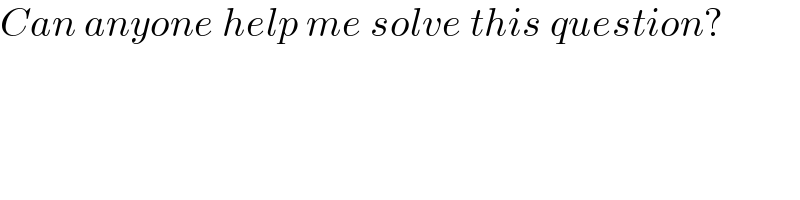
$${Can}\:{anyone}\:{help}\:{me}\:{solve}\:{this}\:{question}? \\ $$
Answered by Rasheed.Sindhi last updated on 07/Sep/22

$${S}_{{n}} =\frac{{n}}{\mathrm{2}}\left({a}+{l}\right)\:;\:{a}:\:{first}\:{term},\:{l}={last}\:{term} \\ $$$${S}_{{p}} =\frac{{p}}{\mathrm{2}}\left({a}+{l}\right)…………..\left({i}\right) \\ $$$${S}_{{p}} =\frac{{q}−\mathrm{3}}{\mathrm{2}}\left({a}+{l}\right)\:;\:{l}=\mathrm{13}…..\left({ii}\right) \\ $$$${Comparing}\:\left({i}\right)\:\&\:\left({ii}\right): \\ $$$${p}={q}−\mathrm{3}\Rightarrow{q}={p}+\mathrm{3} \\ $$
Answered by Cesar1994 last updated on 07/Sep/22
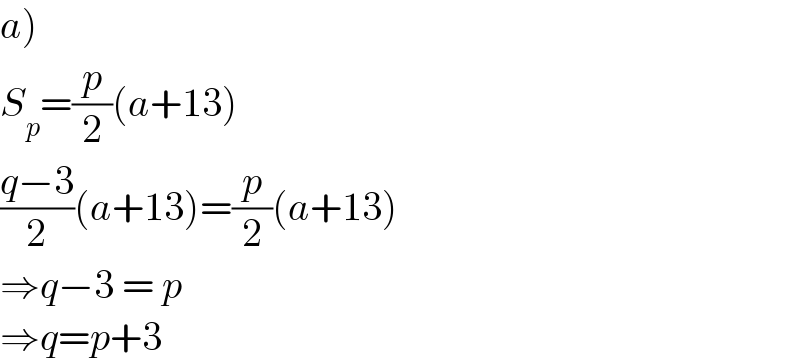
$$\left.{a}\right) \\ $$$${S}_{{p}} =\frac{{p}}{\mathrm{2}}\left({a}+\mathrm{13}\right) \\ $$$$\frac{{q}−\mathrm{3}}{\mathrm{2}}\left({a}+\mathrm{13}\right)=\frac{{p}}{\mathrm{2}}\left({a}+\mathrm{13}\right) \\ $$$$\Rightarrow{q}−\mathrm{3}\:=\:{p} \\ $$$$\Rightarrow{q}={p}+\mathrm{3} \\ $$
