Menu Close

Question-175836

Tinku Tara 0 Comments
Pin




Question Number 175836 by ajfour last updated on 08/Sep/22
Commented by ajfour last updated on 08/Sep/22
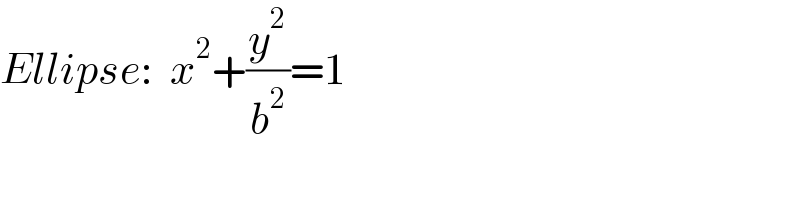
Ellipse: x^2 +(y^2 /b^2 )=1
$${Ellipse}:\:\:{x}^{\mathrm{2}} +\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$
Answered by mr W last updated on 08/Sep/22
Commented by mr W last updated on 08/Sep/22
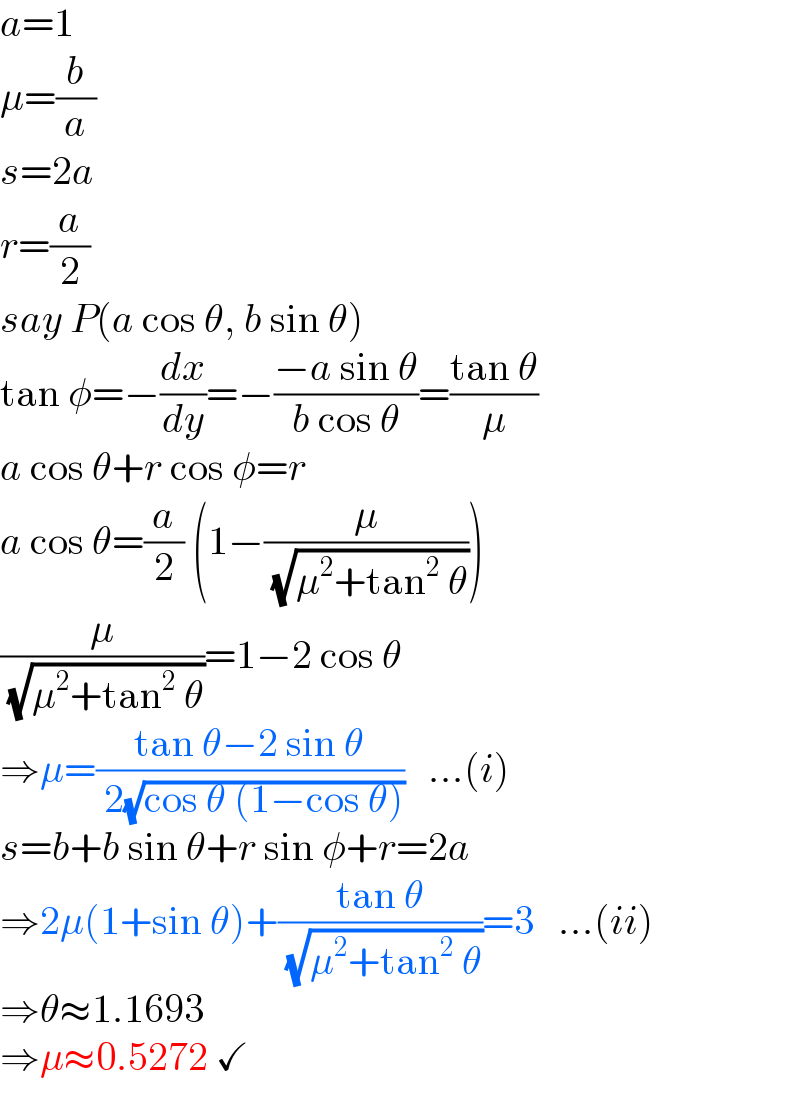
a=1 μ=(b/a) s=2a r=(a/2) say P(a cos θ, b sin θ) tan φ=−(dx/dy)=−((−a sin θ)/(b cos θ))=((tan θ)/μ) a cos θ+r cos φ=r a cos θ=(a/2) (1−(μ/( (√(μ^2 +tan^2 θ))))) (μ/( (√(μ^2 +tan^2 θ))))=1−2 cos θ ⇒μ=((tan θ−2 sin θ)/( 2(√(cos θ (1−cos θ))))) ...(i) s=b+b sin θ+r sin φ+r=2a ⇒2μ(1+sin θ)+((tan θ)/( (√(μ^2 +tan^2 θ))))=3 ...(ii) ⇒θ≈1.1693 ⇒μ≈0.5272 ✓
$${a}=\mathrm{1} \\ $$$$\mu=\frac{{b}}{{a}} \\ $$$${s}=\mathrm{2}{a} \\ $$$${r}=\frac{{a}}{\mathrm{2}} \\ $$$${say}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\phi=−\frac{{dx}}{{dy}}=−\frac{−{a}\:\mathrm{sin}\:\theta}{{b}\:\mathrm{cos}\:\theta}=\frac{\mathrm{tan}\:\theta}{\mu} \\ $$$${a}\:\mathrm{cos}\:\theta+{r}\:\mathrm{cos}\:\phi={r} \\ $$$${a}\:\mathrm{cos}\:\theta=\frac{{a}}{\mathrm{2}}\:\left(\mathrm{1}−\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}\right) \\ $$$$\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}=\mathrm{1}−\mathrm{2}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mu=\frac{\mathrm{tan}\:\theta−\mathrm{2}\:\mathrm{sin}\:\theta}{\:\mathrm{2}\sqrt{\mathrm{cos}\:\theta\:\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}}\:\:\:…\left({i}\right) \\ $$$${s}={b}+{b}\:\mathrm{sin}\:\theta+{r}\:\mathrm{sin}\:\phi+{r}=\mathrm{2}{a} \\ $$$$\Rightarrow\mathrm{2}\mu\left(\mathrm{1}+\mathrm{sin}\:\theta\right)+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}=\mathrm{3}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\theta\approx\mathrm{1}.\mathrm{1693} \\ $$$$\Rightarrow\mu\approx\mathrm{0}.\mathrm{5272}\:\checkmark \\ $$
Commented by Tawa11 last updated on 08/Sep/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 09/Sep/22
Answered by ajfour last updated on 09/Sep/22
Commented by ajfour last updated on 10/Sep/22
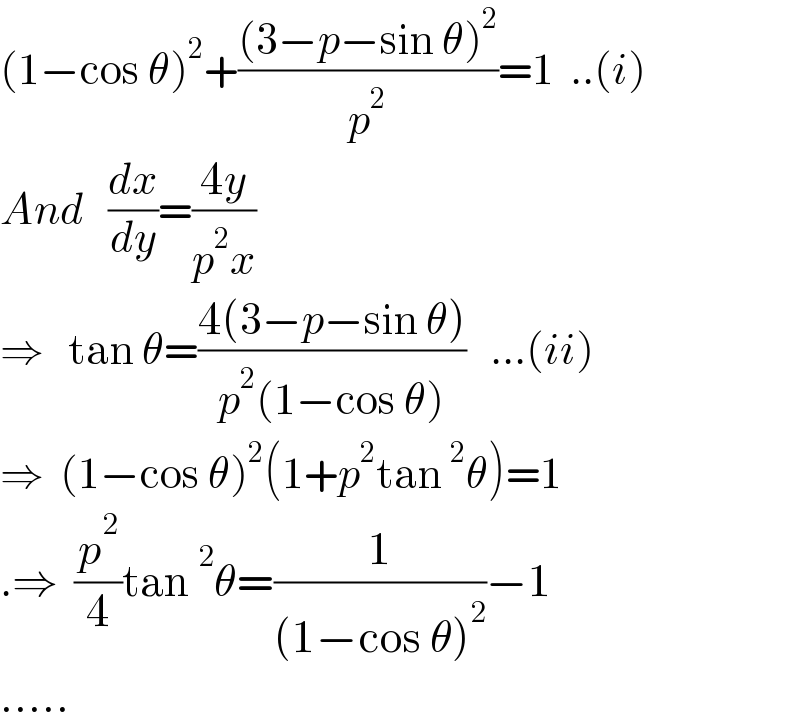
(1−cos θ)^2 +(((3−p−sin θ)^2 )/p^2 )=1 ..(i) And (dx/dy)=((4y)/(p^2 x)) ⇒ tan θ=((4(3−p−sin θ))/(p^2 (1−cos θ))) ...(ii) ⇒ (1−cos θ)^2 (1+p^2 tan^2 θ)=1 .⇒ (p^2 /4)tan^2 θ=(1/((1−cos θ)^2 ))−1 .....
$$\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\frac{\left(\mathrm{3}−{p}−\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{p}^{\mathrm{2}} }=\mathrm{1}\:\:..\left({i}\right) \\ $$$${And}\:\:\:\frac{{dx}}{{dy}}=\frac{\mathrm{4}{y}}{{p}^{\mathrm{2}} {x}} \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\theta=\frac{\mathrm{4}\left(\mathrm{3}−{p}−\mathrm{sin}\:\theta\right)}{{p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \left(\mathrm{1}+{p}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta\right)=\mathrm{1} \\ $$$$.\Rightarrow\:\:\frac{{p}^{\mathrm{2}} }{\mathrm{4}}\mathrm{tan}\:^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} }−\mathrm{1} \\ $$$$….. \\ $$
Commented by mr W last updated on 09/Sep/22
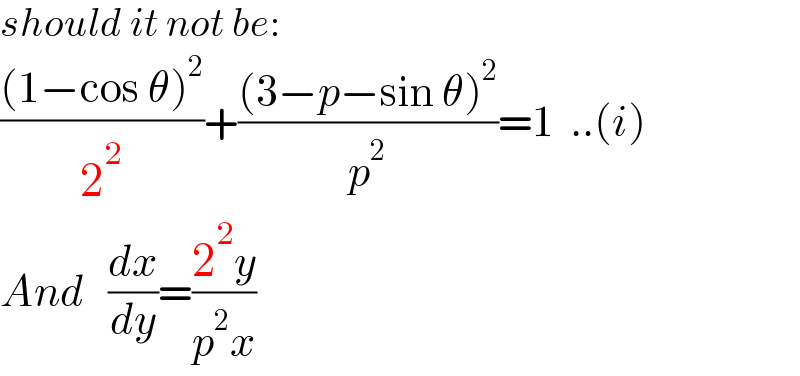
should it not be: (((1−cos θ)^2 )/2^2 )+(((3−p−sin θ)^2 )/p^2 )=1 ..(i) And (dx/dy)=((2^2 y)/(p^2 x))
$${should}\:{it}\:{not}\:{be}: \\ $$$$\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{\left(\mathrm{3}−{p}−\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{p}^{\mathrm{2}} }=\mathrm{1}\:\:..\left({i}\right) \\ $$$${And}\:\:\:\frac{{dx}}{{dy}}=\frac{\mathrm{2}^{\mathrm{2}} {y}}{{p}^{\mathrm{2}} {x}} \\ $$
Commented by ajfour last updated on 09/Sep/22
yez, thanks sir.
$${yez},\:{thanks}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *