Question-176211

Question Number 176211 by adhigenz last updated on 15/Sep/22

Answered by mahdipoor last updated on 15/Sep/22

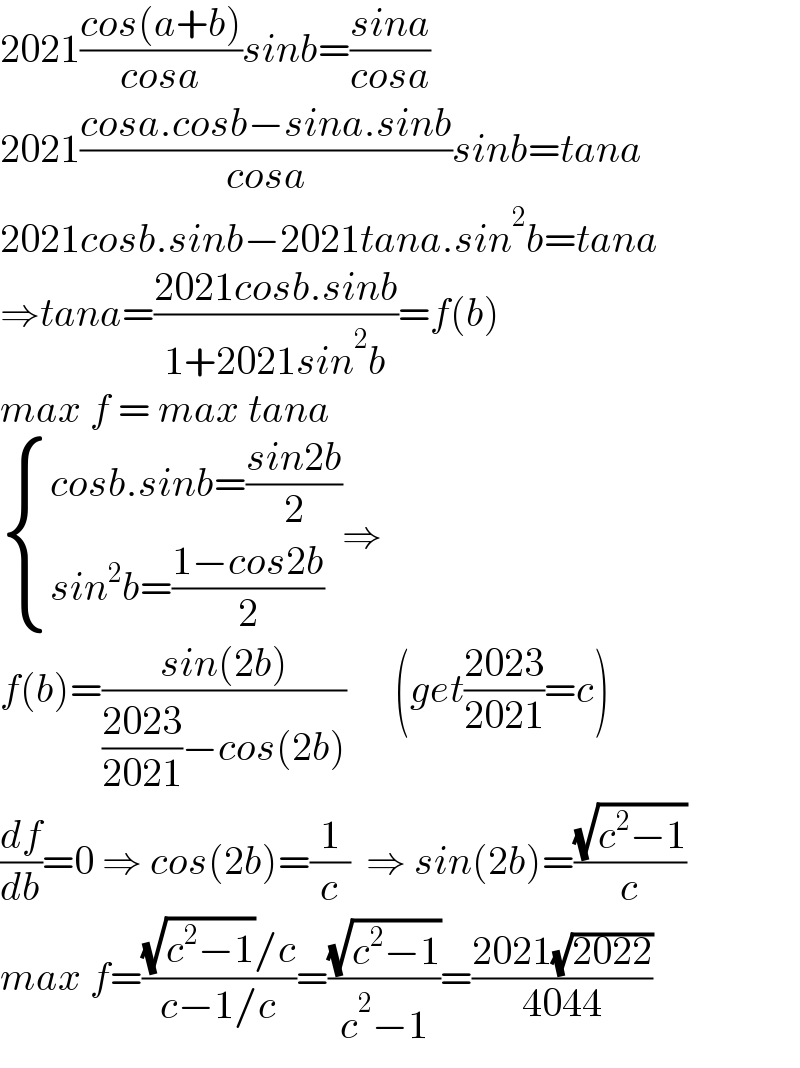
2021((cos(a+b))/(cosa))sinb=((sina)/(cosa)) 2021((cosa.cosb−sina.sinb)/(cosa))sinb=tana 2021cosb.sinb−2021tana.sin^2 b=tana ⇒tana=((2021cosb.sinb)/(1+2021sin^2 b))=f(b) max f = max tana { ((cosb.sinb=((sin2b)/2))),((sin^2 b=((1−cos2b)/2))) :}⇒ f(b)=((sin(2b))/(((2023)/(2021))−cos(2b))) (get((2023)/(2021))=c) (df/db)=0 ⇒ cos(2b)=(1/c) ⇒ sin(2b)=((√(c^2 −1))/c) max f=(((√(c^2 −1))/c)/(c−1/c))=((√(c^2 −1))/(c^2 −1))=((2021(√(2022)))/(4044))

$$\mathrm{2021}\frac{{cos}\left({a}+{b}\right)}{{cosa}}{sinb}=\frac{{sina}}{{cosa}} \\ $$$$\mathrm{2021}\frac{{cosa}.{cosb}−{sina}.{sinb}}{{cosa}}{sinb}={tana} \\ $$$$\mathrm{2021}{cosb}.{sinb}−\mathrm{2021}{tana}.{sin}^{\mathrm{2}} {b}={tana} \\ $$$$\Rightarrow{tana}=\frac{\mathrm{2021}{cosb}.{sinb}}{\mathrm{1}+\mathrm{2021}{sin}^{\mathrm{2}} {b}}={f}\left({b}\right) \\ $$$${max}\:{f}\:=\:{max}\:{tana} \\ $$$$\begin{cases}{{cosb}.{sinb}=\frac{{sin}\mathrm{2}{b}}{\mathrm{2}}}\\{{sin}^{\mathrm{2}} {b}=\frac{\mathrm{1}−{cos}\mathrm{2}{b}}{\mathrm{2}}}\end{cases}\Rightarrow \\ $$$${f}\left({b}\right)=\frac{{sin}\left(\mathrm{2}{b}\right)}{\frac{\mathrm{2023}}{\mathrm{2021}}−{cos}\left(\mathrm{2}{b}\right)}\:\:\:\:\:\:\left({get}\frac{\mathrm{2023}}{\mathrm{2021}}={c}\right) \\ $$$$\frac{{df}}{{db}}=\mathrm{0}\:\Rightarrow\:{cos}\left(\mathrm{2}{b}\right)=\frac{\mathrm{1}}{{c}}\:\:\Rightarrow\:{sin}\left(\mathrm{2}{b}\right)=\frac{\sqrt{{c}^{\mathrm{2}} −\mathrm{1}}}{{c}} \\ $$$${max}\:{f}=\frac{\sqrt{{c}^{\mathrm{2}} −\mathrm{1}}/{c}}{{c}−\mathrm{1}/{c}}=\frac{\sqrt{{c}^{\mathrm{2}} −\mathrm{1}}}{{c}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2021}\sqrt{\mathrm{2022}}}{\mathrm{4044}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply