Question Number 176274 by mnjuly1970 last updated on 15/Sep/22
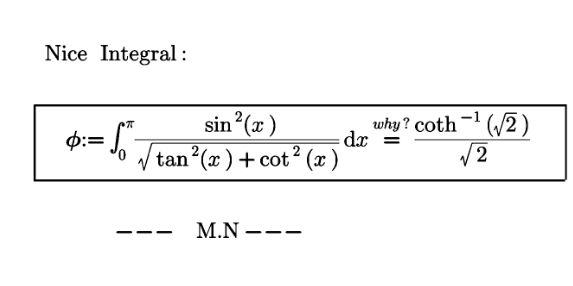
Answered by Frix last updated on 16/Sep/22
![y=coth x ⇔ x=(1/2)ln ((y+1)/(y−1)) (1/( (√2)))coth^(−1) (√2) =((√2)/2)ln (1+(√2)) ∫_0 ^π ((sin^2 x)/( (√(tan^2 x +cot^2 x))))dx=2∫_0 ^(π/2) ((sin^2 x)/( (√(tan^2 x +cot^2 x))))dx= =2∫_0 ^(π/2) ((tan^2 x)/((1+tan^2 x)(√(1+tan^4 x))))tan x dx t=tan^2 x dx=(dt/(2(1+tan^2 x)tan x)) now we have ∫_0 ^∞ (t/((t+1)^2 (√(t^2 +1))))dt u=t+(√(t^2 +1)) dt=((√(t^2 +1))/u)du now we have 2∫_1 ^∞ ((u^2 −1)/((u^2 +2u−1)^2 ))du= =[((1−u)/(u^2 +2u−1))+((√2)/4)ln ((u+1−(√2))/(u+1+(√2)))]_1 ^∞ = =((√2)/2)ln (1+(√2))](https://www.tinkutara.com/question/Q176302.png)
$${y}=\mathrm{coth}\:{x}\:\Leftrightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{y}+\mathrm{1}}{{y}−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{coth}^{−\mathrm{1}} \:\sqrt{\mathrm{2}}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\:\sqrt{\mathrm{tan}^{\mathrm{2}} \:{x}\:+\mathrm{cot}^{\mathrm{2}} \:{x}}}{dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\:\sqrt{\mathrm{tan}^{\mathrm{2}} \:{x}\:+\mathrm{cot}^{\mathrm{2}} \:{x}}}{dx}= \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{tan}^{\mathrm{2}} \:{x}}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right)\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{4}} \:{x}}}\mathrm{tan}\:{x}\:{dx} \\ $$$${t}=\mathrm{tan}^{\mathrm{2}} \:{x} \\ $$$${dx}=\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right)\mathrm{tan}\:{x}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt} \\ $$$${u}={t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${dt}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{u}}{du} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2}\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{1}\right)^{\mathrm{2}} }{du}= \\ $$$$=\left[\frac{\mathrm{1}−{u}}{{u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{1}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\frac{{u}+\mathrm{1}−\sqrt{\mathrm{2}}}{{u}+\mathrm{1}+\sqrt{\mathrm{2}}}\right]_{\mathrm{1}} ^{\infty} = \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Commented by Tawa11 last updated on 18/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
