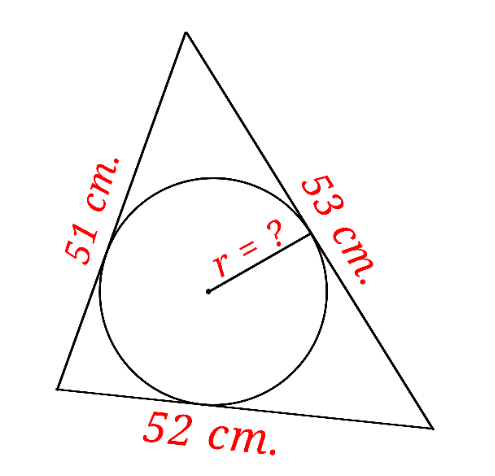
Question Number 176354 by BaliramKumar last updated on 16/Sep/22
Answered by Frix last updated on 16/Sep/22
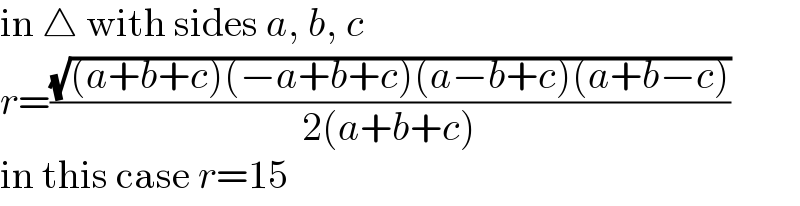
$$\mathrm{in}\:\bigtriangleup\:\mathrm{with}\:\mathrm{sides}\:{a},\:{b},\:{c} \\ $$$${r}=\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{2}\left({a}+{b}+{c}\right)} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{r}=\mathrm{15} \\ $$
Commented by BaliramKumar last updated on 16/Sep/22

$${thanks} \\ $$
Answered by behi834171 last updated on 16/Sep/22
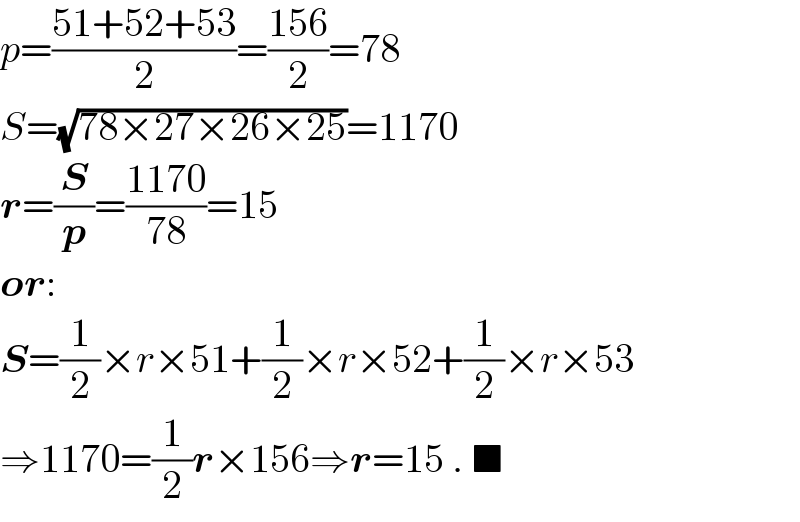
$${p}=\frac{\mathrm{51}+\mathrm{52}+\mathrm{53}}{\mathrm{2}}=\frac{\mathrm{156}}{\mathrm{2}}=\mathrm{78} \\ $$$${S}=\sqrt{\mathrm{78}×\mathrm{27}×\mathrm{26}×\mathrm{25}}=\mathrm{1170} \\ $$$$\boldsymbol{{r}}=\frac{\boldsymbol{{S}}}{\boldsymbol{{p}}}=\frac{\mathrm{1170}}{\mathrm{78}}=\mathrm{15} \\ $$$$\boldsymbol{{or}}: \\ $$$$\boldsymbol{{S}}=\frac{\mathrm{1}}{\mathrm{2}}×{r}×\mathrm{51}+\frac{\mathrm{1}}{\mathrm{2}}×{r}×\mathrm{52}+\frac{\mathrm{1}}{\mathrm{2}}×{r}×\mathrm{53} \\ $$$$\Rightarrow\mathrm{1170}=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{r}}×\mathrm{156}\Rightarrow\boldsymbol{{r}}=\mathrm{15}\:.\:\blacksquare \\ $$
Commented by BaliramKumar last updated on 16/Sep/22

$${thanks} \\ $$
