Question-176391

Question Number 176391 by cortano1 last updated on 18/Sep/22

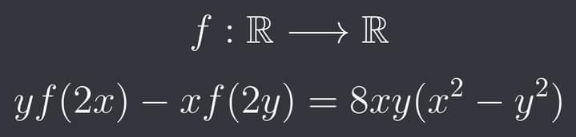
Commented by mr W last updated on 18/Sep/22

$${f}\left({x}\right)={x}^{\mathrm{3}} \\ $$

Answered by TheHoneyCat last updated on 18/Sep/22

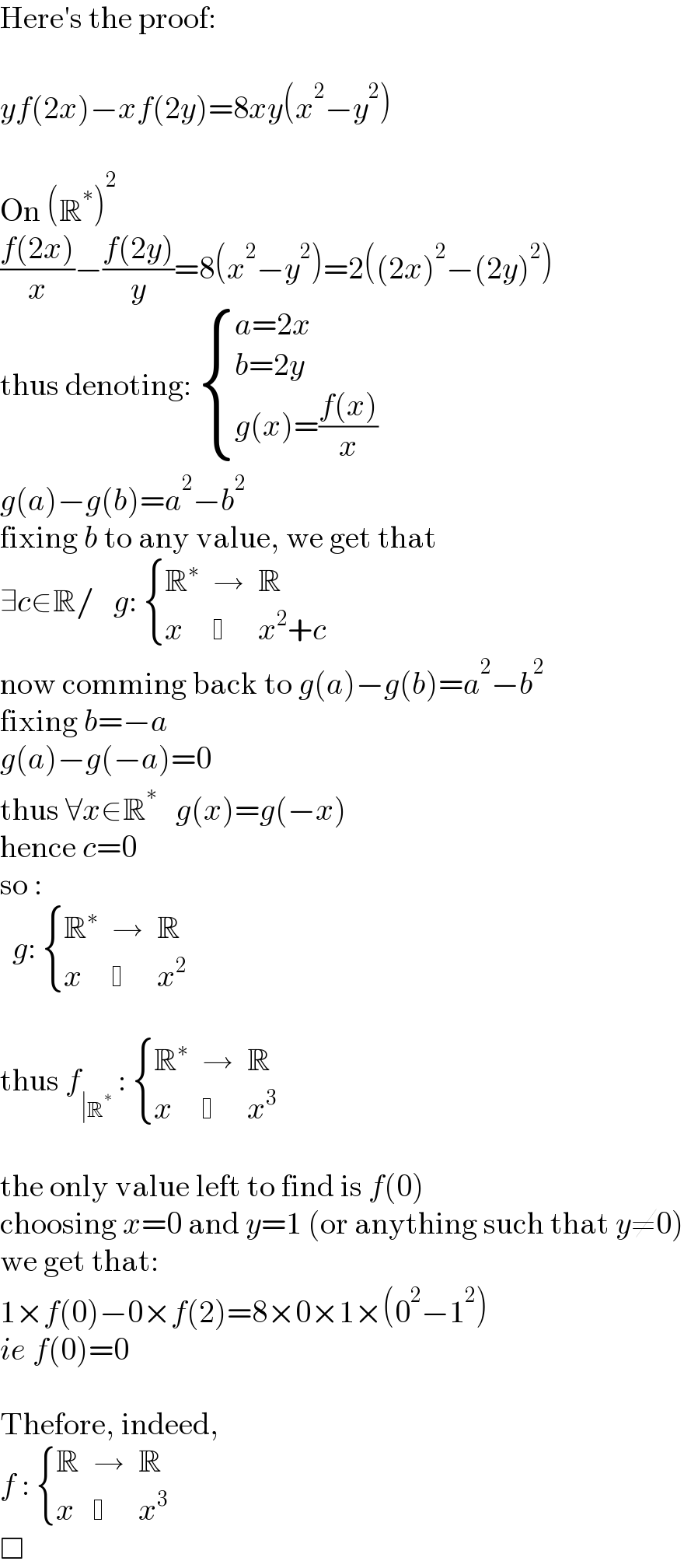
Here′s the proof: yf(2x)−xf(2y)=8xy(x^2 −y^2 ) On (R^∗ )^2 ((f(2x))/x)−((f(2y))/y)=8(x^2 −y^2 )=2((2x)^2 −(2y)^2 ) thus denoting: { ((a=2x)),((b=2y)),((g(x)=((f(x))/x))) :} g(a)−g(b)=a^2 −b^2 fixing b to any value, we get that ∃c∈R/ g: { (R^∗ ,→,R),(x, ,(x^2 +c)) :} now comming back to g(a)−g(b)=a^2 −b^2 fixing b=−a g(a)−g(−a)=0 thus ∀x∈R^∗ g(x)=g(−x) hence c=0 so : g: { (R^∗ ,→,R),(x, ,x^2 ) :} thus f_(∣R^∗ ) : { (R^∗ ,→,R),(x, ,x^3 ) :} the only value left to find is f(0) choosing x=0 and y=1 (or anything such that y≠0) we get that: 1×f(0)−0×f(2)=8×0×1×(0^2 −1^2 ) ie f(0)=0 Thefore, indeed, f : { (R,→,R),(x, ,x^3 ) :} □

$$\mathrm{Here}'\mathrm{s}\:\mathrm{the}\:\mathrm{proof}: \\ $$$$ \\ $$$${yf}\left(\mathrm{2}{x}\right)−{xf}\left(\mathrm{2}{y}\right)=\mathrm{8}{xy}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$\mathrm{On}\:\left(\mathbb{R}^{\ast} \right)^{\mathrm{2}} \\ $$$$\frac{{f}\left(\mathrm{2}{x}\right)}{{x}}−\frac{{f}\left(\mathrm{2}{y}\right)}{{y}}=\mathrm{8}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)=\mathrm{2}\left(\left(\mathrm{2}{x}\right)^{\mathrm{2}} −\left(\mathrm{2}{y}\right)^{\mathrm{2}} \right) \\ $$$$\mathrm{thus}\:\mathrm{denoting}:\:\begin{cases}{{a}=\mathrm{2}{x}}\\{{b}=\mathrm{2}{y}}\\{{g}\left({x}\right)=\frac{{f}\left({x}\right)}{{x}}}\end{cases} \\ $$$${g}\left({a}\right)−{g}\left({b}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\mathrm{fixing}\:{b}\:\mathrm{to}\:\mathrm{any}\:\mathrm{value},\:\mathrm{we}\:\mathrm{get}\:\mathrm{that} \\ $$$$\exists{c}\in\mathbb{R}/\:\:\:{g}:\:\begin{cases}{\mathbb{R}^{\ast} }&{\rightarrow}&{\mathbb{R}}\\{{x}}&{ }&{{x}^{\mathrm{2}} +{c}}\end{cases} \\ $$$$\mathrm{now}\:\mathrm{comming}\:\mathrm{back}\:\mathrm{to}\:{g}\left({a}\right)−{g}\left({b}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\mathrm{fixing}\:{b}=−{a} \\ $$$${g}\left({a}\right)−{g}\left(−{a}\right)=\mathrm{0} \\ $$$$\mathrm{thus}\:\forall{x}\in\mathbb{R}^{\ast} \:\:\:{g}\left({x}\right)={g}\left(−{x}\right) \\ $$$$\mathrm{hence}\:{c}=\mathrm{0} \\ $$$$\mathrm{so}\:: \\ $$$$\:\:{g}:\:\begin{cases}{\mathbb{R}^{\ast} }&{\rightarrow}&{\mathbb{R}}\\{{x}}&{ }&{{x}^{\mathrm{2}} }\end{cases} \\ $$$$ \\ $$$$\mathrm{thus}\:{f}_{\mid\mathbb{R}^{\ast} } \::\:\begin{cases}{\mathbb{R}^{\ast} }&{\rightarrow}&{\mathbb{R}}\\{{x}}&{ }&{{x}^{\mathrm{3}} }\end{cases} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{value}\:\mathrm{left}\:\mathrm{to}\:\mathrm{find}\:\mathrm{is}\:{f}\left(\mathrm{0}\right) \\ $$$$\mathrm{choosing}\:{x}=\mathrm{0}\:\mathrm{and}\:{y}=\mathrm{1}\:\left(\mathrm{or}\:\mathrm{anything}\:\mathrm{such}\:\mathrm{that}\:{y}\neq\mathrm{0}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{that}: \\ $$$$\mathrm{1}×{f}\left(\mathrm{0}\right)−\mathrm{0}×{f}\left(\mathrm{2}\right)=\mathrm{8}×\mathrm{0}×\mathrm{1}×\left(\mathrm{0}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} \right) \\ $$$${ie}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Thefore},\:\mathrm{indeed},\: \\ $$$${f}\::\:\begin{cases}{\mathbb{R}}&{\rightarrow}&{\mathbb{R}}\\{{x}}&{ }&{{x}^{\mathrm{3}} }\end{cases} \\ $$$$\Box \\ $$

Answered by mr W last updated on 19/Sep/22

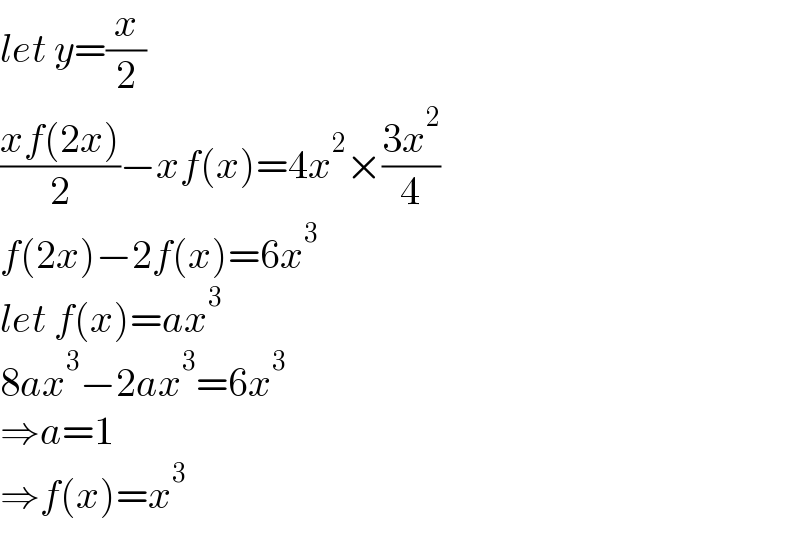
let y=(x/2) ((xf(2x))/2)−xf(x)=4x^2 ×((3x^2 )/4) f(2x)−2f(x)=6x^3 let f(x)=ax^3 8ax^3 −2ax^3 =6x^3 ⇒a=1 ⇒f(x)=x^3

$${let}\:{y}=\frac{{x}}{\mathrm{2}} \\ $$$$\frac{{xf}\left(\mathrm{2}{x}\right)}{\mathrm{2}}−{xf}\left({x}\right)=\mathrm{4}{x}^{\mathrm{2}} ×\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${f}\left(\mathrm{2}{x}\right)−\mathrm{2}{f}\left({x}\right)=\mathrm{6}{x}^{\mathrm{3}} \\ $$$${let}\:{f}\left({x}\right)={ax}^{\mathrm{3}} \\ $$$$\mathrm{8}{ax}^{\mathrm{3}} −\mathrm{2}{ax}^{\mathrm{3}} =\mathrm{6}{x}^{\mathrm{3}} \\ $$$$\Rightarrow{a}=\mathrm{1} \\ $$$$\Rightarrow{f}\left({x}\right)={x}^{\mathrm{3}} \\ $$

Commented by Tawa11 last updated on 20/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply