Menu Close

Question-176485

Tinku Tara 0 Comments
Pin




Question Number 176485 by Shrinava last updated on 20/Sep/22
Commented by mr W last updated on 20/Sep/22
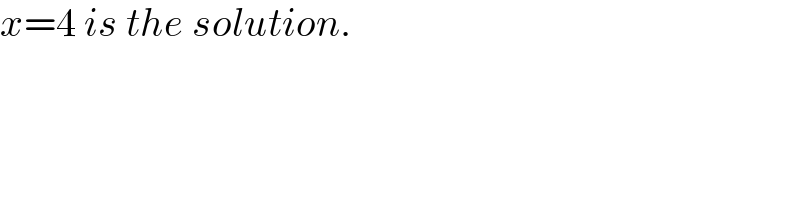
x=4 is the solution.
$${x}=\mathrm{4}\:{is}\:{the}\:{solution}. \\ $$
Answered by a.lgnaoui last updated on 20/Sep/22
∫((t^2 +1)/(t^3 +1))dt=∫(t^2 /(t^3 +1))+∫(1/(t^3 +1))dt =(1/2)∫((2t^2 )/(1+t^3 ))dt+∫(1/((t+1)(t^2 −t+1)))dt ∫(1/(t+1)(t^2 −t+1)))dt=(1/3)∫((1/(t+1))+((2−t)/(t^2 −t+1)))dt ∫((2−t)/(t^2 −t+1))dt=∫((−(t−(1/2))+(3/2))/((t−(1/2))^2 +(3/4)))dt =−(1/2)∫((2t−1)/(t^2 −t+1))+(3/2)×(4/3)∫(dt/([(2/( (√3)))(t−(1/2))]^2 +1)) =−(1/2)log(t^2 −t+1)+2Arctan [((√3)/3)(2t−1)] finalement I=(1/2)log(1+t^3 )+(1/3)log(1+t)−(1/2)log(t^2 −t+1)+(1/3)2Arctan [((√3)/3)(2t−1) ∫_4 ^x ((t^2 +1)/(t^3 +1))dt=(1/2)[((log(1+t^3 )]_4 ^x −log(1−t+t^2 ))]_4 ^x +(1/3)[log(1+t)]_4 ^x +(2/3)Arc[((√3)/3)(2t−1)]_4 ^x =(1/2)[log(((1+t^3 )/(1−t+t^2 )))]_4 ^x +(1/3)[log(1+t)]_4 ^x +(2/3)Arctan [((√3)/3)(2t−1)]_4^ ^x =(1/2)[log(1+t)]_4 ^x +(1/3)[log(1+t)]_4 ^x +(2/3)Arctan [((√3)/3)(2t−1)]_4 ^x (5/6)[log(1+x)−log5)]+(2/3)[Arctan (((√3)/3)2x−((√3)/3))−(2/3)Arctan ((7(√3))/3) (5/6)log(((1+x)/5))+(2/3)Arctan (((2(√3))/3) x−((√3)/3))−(2/3)Arctan (((7(√3))/3)) I=2((√x) −2) 1+x=1+((√x) )^2 (√x) =X log[((1+x)/5)]^(5/6) −2(√x) +Arctan ((√3)/3)(2x−1)=4+(2/4)Arctan( ((7(√3))/3)) log(((1+X^2 )/5))^(5/6) −2X+Arctan ((√3)/3)(2X^2 −1)−4−Arctan (((7(√3))/3))=0 ...
$$\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{3}} +\mathrm{1}}{dt}=\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{3}} +\mathrm{1}}+\int\frac{\mathrm{1}}{{t}^{\mathrm{3}} +\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{3}} }{dt}+\int\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}{dt} \\ $$$$\int\frac{\mathrm{1}}{\left.{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}{dt}=\frac{\mathrm{1}}{\mathrm{3}}\int\left(\frac{\mathrm{1}}{{t}+\mathrm{1}}+\frac{\mathrm{2}−{t}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}\right){dt} \\ $$$$\int\frac{\mathrm{2}−{t}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt}=\int\frac{−\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{3}}{\mathrm{2}}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}\int\frac{{dt}}{\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]^{\mathrm{2}} +\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)+\mathrm{2Arctan}\:\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)\right] \\ $$$${finalement} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{1}+\mathrm{t}^{\mathrm{3}} \right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{2Arctan}\:\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2t}−\mathrm{1}\right)\right. \\ $$$$\int_{\mathrm{4}} ^{{x}} \frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{3}} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\left(\mathrm{log}\left(\mathrm{1}+\mathrm{t}^{\mathrm{3}} \right)\right]_{\mathrm{4}} ^{\mathrm{x}} −\mathrm{log}\left(\mathrm{1}−\mathrm{t}+\mathrm{t}^{\mathrm{2}} \right)\right)\right]_{\mathrm{4}} ^{\mathrm{x}} +\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)\right]_{\mathrm{4}} ^{\mathrm{x}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{Arc}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2t}−\mathrm{1}\right)\right]_{\mathrm{4}} ^{\mathrm{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{log}\left(\frac{\mathrm{1}+\mathrm{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{t}+\mathrm{t}^{\mathrm{2}} }\right)\right]_{\mathrm{4}} ^{\mathrm{x}} +\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)\right]_{\mathrm{4}} ^{\mathrm{x}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{A}{rc}\mathrm{tan}\:\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)\right]_{\mathrm{4}^{} } ^{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)\right]_{\mathrm{4}} ^{\mathrm{x}} +\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)\right]_{\mathrm{4}} ^{\mathrm{x}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{A}{rc}\mathrm{tan}\:\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)\right]_{\mathrm{4}} ^{{x}} \\ $$$$\left.\frac{\mathrm{5}}{\mathrm{6}}\left[\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{log5}\right)\right]+\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{Arctan}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{2x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{A}{rc}\mathrm{tan}\:\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{3}}\right. \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}\left(\frac{\mathrm{1}+\mathrm{x}}{\mathrm{5}}\right)+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{A}{rc}\mathrm{tan}\:\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)−\frac{\mathrm{2}}{\mathrm{3}}{Arc}\mathrm{tan}\:\left(\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{3}}\right) \\ $$$${I}=\mathrm{2}\left(\sqrt{{x}}\:−\mathrm{2}\right)\:\:\:\:\:\mathrm{1}+{x}=\mathrm{1}+\left(\sqrt{{x}}\:\right)^{\mathrm{2}} \:\:\:\sqrt{{x}}\:={X} \\ $$$$ \\ $$$$\mathrm{log}\left[\frac{\mathrm{1}+\mathrm{x}}{\mathrm{5}}\right]^{\frac{\mathrm{5}}{\mathrm{6}}} −\mathrm{2}\sqrt{\mathrm{x}}\:+\mathrm{A}{rc}\mathrm{tan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{4}+\frac{\mathrm{2}}{\mathrm{4}}{Arc}\mathrm{tan}\left(\:\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{3}}\right) \\ $$$$\:\mathrm{log}\left(\frac{\mathrm{1}+\mathrm{X}^{\mathrm{2}} }{\mathrm{5}}\right)^{\frac{\mathrm{5}}{\mathrm{6}}} −\mathrm{2}{X}+{Ar}\mathrm{ctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{X}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{4}−{Arc}\mathrm{tan}\:\left(\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$… \\ $$$$ \\ $$
Commented by Shrinava last updated on 20/Sep/22
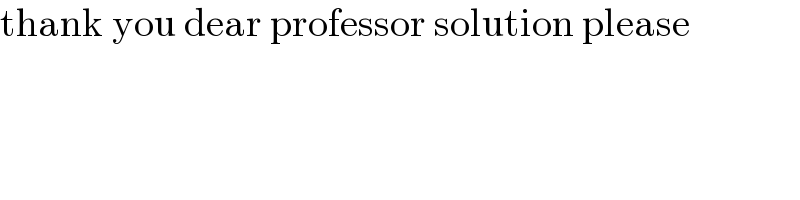
thank you dear professor solution please
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{solution}\:\mathrm{please} \\ $$
Commented by a.lgnaoui last updated on 20/Sep/22
x=4
$${x}=\mathrm{4} \\ $$
Answered by Peace last updated on 20/Sep/22
F(x)=∫_4 ^x ((t^2 +1)/(t^3 +1))dt−2((√x)−2),DF=R_+ F′(x)=((x^2 +1)/(x^3 +1))−(1/( (√x))),∀x∈R_+ ^∗ g(x)=F^′ (x^2 )=((x^4 +1)/(x^6 +1))−(1/x)=((x^5 +x−x^6 −1)/(x(x^6 +1)))=(((x−1)(x^5 −1))/(x(x^6 +1))) x_([0,∞[) →^h x^( 2) _([0,∞[) is Bijection =(((x−1)(x−1)(x^4 +x^3 +x^2 +1))/(x(x^6 +1)))=(((x−1)^2 (x^4 +x^3 +x^2 +1))/(x(x^6 +1)))≥0 ∀x∈R_+ ^∗ ⇒F(x) Is increasing Function F(4)=0⇒x=4 is the UniQue solution
$${F}\left({x}\right)=\int_{\mathrm{4}} ^{{x}} \frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{3}} +\mathrm{1}}{dt}−\mathrm{2}\left(\sqrt{{x}}−\mathrm{2}\right),{DF}=\mathbb{R}_{+} \\ $$$${F}'\left({x}\right)=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{3}} +\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{{x}}},\forall{x}\in\mathbb{R}_{+} ^{\ast} \\ $$$${g}\left({x}\right)={F}^{'} \left({x}^{\mathrm{2}} \right)=\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}−\frac{\mathrm{1}}{{x}}=\frac{{x}^{\mathrm{5}} +{x}−\boldsymbol{{x}}^{\mathrm{6}} −\mathrm{1}}{\boldsymbol{{x}}\left(\boldsymbol{{x}}^{\mathrm{6}} +\mathrm{1}\right)}=\frac{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{5}} −\mathrm{1}\right)}{{x}\left({x}^{\mathrm{6}} +\mathrm{1}\right)} \\ $$$$\underset{\left[\mathrm{0},\infty\left[\right.\right.} {{x}}\overset{{h}} {\rightarrow}\underset{\left[\mathrm{0},\infty\left[\right.\right.} {{x}}^{\:\:\:\:\:\mathrm{2}} \:\:{is}\:{Bijection}\: \\ $$$$=\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}\left({x}^{\mathrm{6}} +\mathrm{1}\right)}=\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}\left({x}^{\mathrm{6}} +\mathrm{1}\right)}\geqslant\mathrm{0} \\ $$$$\forall{x}\in\mathbb{R}_{+} ^{\ast} \\ $$$$\Rightarrow{F}\left({x}\right)\:{Is}\:{increasing}\:{Function} \\ $$$${F}\left(\mathrm{4}\right)=\mathrm{0}\Rightarrow{x}=\mathrm{4}\:{is}\:{the}\:{UniQue}\:{solution} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *