Question Number 176595 by MASANJAJJ last updated on 22/Sep/22

Answered by Rasheed.Sindhi last updated on 22/Sep/22
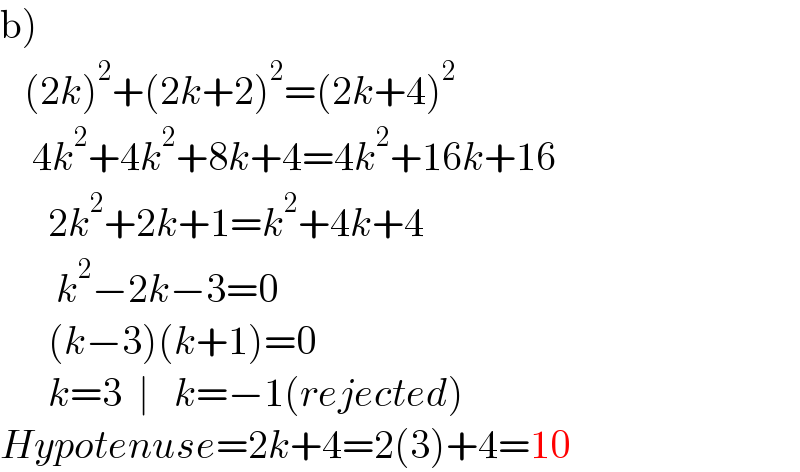
$$\left.\mathrm{b}\right) \\ $$$$\:\:\:\left(\mathrm{2}{k}\right)^{\mathrm{2}} +\left(\mathrm{2}{k}+\mathrm{2}\right)^{\mathrm{2}} =\left(\mathrm{2}{k}+\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{4}{k}^{\mathrm{2}} +\mathrm{4}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{4}=\mathrm{4}{k}^{\mathrm{2}} +\mathrm{16}{k}+\mathrm{16} \\ $$$$\:\:\:\:\:\:\mathrm{2}{k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1}={k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:{k}^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left({k}−\mathrm{3}\right)\left({k}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:{k}=\mathrm{3}\:\:\mid\:\:\:{k}=−\mathrm{1}\left({rejected}\right) \\ $$$${Hypotenuse}=\mathrm{2}{k}+\mathrm{4}=\mathrm{2}\left(\mathrm{3}\right)+\mathrm{4}=\mathrm{10} \\ $$
Answered by Rasheed.Sindhi last updated on 22/Sep/22
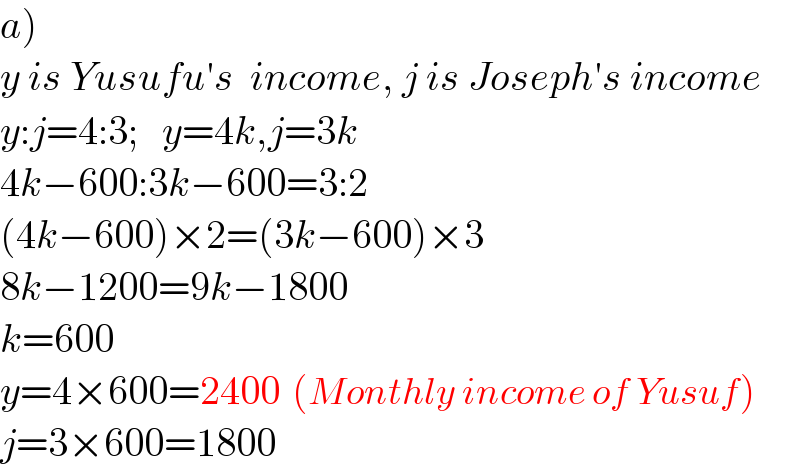
$$\left.{a}\right) \\ $$$${y}\:{is}\:{Yusufu}'{s}\:\:{income},\:{j}\:{is}\:{Joseph}'{s}\:{income} \\ $$$${y}:{j}=\mathrm{4}:\mathrm{3};\:\:\:{y}=\mathrm{4}{k},{j}=\mathrm{3}{k} \\ $$$$\mathrm{4}{k}−\mathrm{600}:\mathrm{3}{k}−\mathrm{600}=\mathrm{3}:\mathrm{2} \\ $$$$\left(\mathrm{4}{k}−\mathrm{600}\right)×\mathrm{2}=\left(\mathrm{3}{k}−\mathrm{600}\right)×\mathrm{3} \\ $$$$\mathrm{8}{k}−\mathrm{1200}=\mathrm{9}{k}−\mathrm{1800} \\ $$$${k}=\mathrm{600} \\ $$$${y}=\mathrm{4}×\mathrm{600}=\mathrm{2400}\:\:\left({Monthly}\:{income}\:{of}\:{Yusuf}\right) \\ $$$${j}=\mathrm{3}×\mathrm{600}=\mathrm{1800} \\ $$
Commented by Tawa11 last updated on 23/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
