Question Number 176692 by mnjuly1970 last updated on 25/Sep/22

Commented by cortano1 last updated on 25/Sep/22

$$\:\Omega\:=\:\mathrm{8}\pi^{\mathrm{4}} \\ $$
Answered by blackmamba last updated on 25/Sep/22
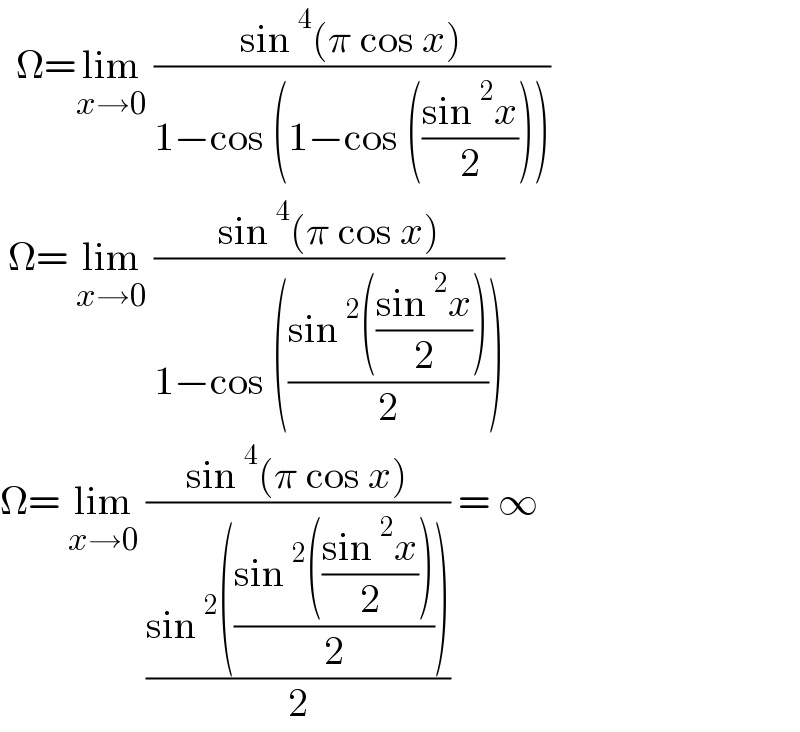
$$\:\:\Omega=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{4}} \left(\pi\:\mathrm{cos}\:{x}\right)}{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{2}}\right)\right)} \\ $$$$\:\Omega=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{4}} \left(\pi\:\mathrm{cos}\:{x}\right)}{\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{2}}\right)}{\mathrm{2}}\right)} \\ $$$$\Omega=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{4}} \left(\pi\:\mathrm{cos}\:{x}\right)}{\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{2}}\right)}{\mathrm{2}}\right)}{\mathrm{2}}}\:=\:\infty \\ $$
