Question Number 176721 by youssefelaour last updated on 25/Sep/22
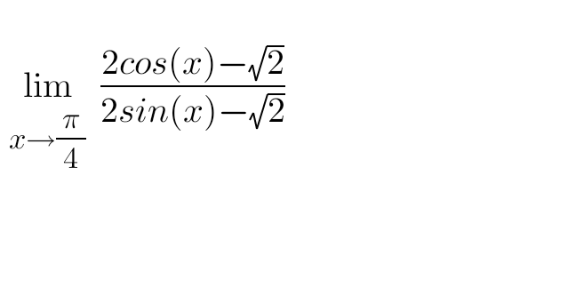
Answered by MJS_new last updated on 25/Sep/22

$$=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:{x}}{\mathrm{2cos}\:{x}}\:=−\mathrm{1} \\ $$
Answered by cortano1 last updated on 26/Sep/22

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)−\sqrt{\mathrm{2}}}{\mathrm{2sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)−\sqrt{\mathrm{2}}}\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left\{\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{x}\right\}−\sqrt{\mathrm{2}}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x}\right)−\sqrt{\mathrm{2}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\:\left(\mathrm{cos}\:\mathrm{x}−\mathrm{1}\right)−\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\:\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\sqrt{\mathrm{2}}\:\left(\mathrm{cos}\:\mathrm{x}−\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\left(\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}{\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\left(\mathrm{cos}\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}=\:−\mathrm{1} \\ $$
