Question-17676

Question Number 17676 by mondodotto@gmail.com last updated on 09/Jul/17

Answered by alex041103 last updated on 09/Jul/17

First: ((5cos^3 x + 2sin^3 x)/(2sin^2 xcos^2 x)) = (5/2) ((cosx)/(sin^2 x))+((sinx)/(cos^2 x)) ⇒I= ∫ ((5cos^3 x + 2sin^3 x)/(2sin^2 xcos^2 x))= =(5/2)∫ ((cosx)/(sin^2 x))dx + ∫ ((sinx)/(cos^2 x))dx No We substitute for the first integral u=sinx→du=cosxdx And for the second w=cosx→dw=−sinxdx ⇒I=(5/2)∫u^(−2) du − ∫w^(−2) dw= =−(5/(2sinx)) + (1/(cosx)) + C ⇒I=∫((5cos^3 x+2sin^3 x)/(2sin^2 xcos^2 x)) dx = (1/(cosx))−(5/(2sinx))+C

$$\mathrm{First}: \\ $$$$\frac{\mathrm{5cos}^{\mathrm{3}} \mathrm{x}\:+\:\mathrm{2sin}^{\mathrm{3}} \mathrm{x}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{xcos}^{\mathrm{2}} \mathrm{x}}\:=\:\frac{\mathrm{5}}{\mathrm{2}}\:\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\Rightarrow\mathrm{I}=\:\int\:\frac{\mathrm{5cos}^{\mathrm{3}} \mathrm{x}\:+\:\mathrm{2sin}^{\mathrm{3}} \mathrm{x}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{xcos}^{\mathrm{2}} \mathrm{x}}= \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\:\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:+\:\int\:\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{No}\:\mathrm{We}\:\mathrm{substitute}\:\mathrm{for}\:\mathrm{the}\:\mathrm{first}\:\mathrm{integral} \\ $$$$\mathrm{u}=\mathrm{sinx}\rightarrow\mathrm{du}=\mathrm{cosxdx} \\ $$$$\mathrm{And}\:\mathrm{for}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{w}=\mathrm{cosx}\rightarrow\mathrm{dw}=−\mathrm{sinxdx} \\ $$$$\Rightarrow\mathrm{I}=\frac{\mathrm{5}}{\mathrm{2}}\int\mathrm{u}^{−\mathrm{2}} \mathrm{du}\:−\:\int\mathrm{w}^{−\mathrm{2}} \mathrm{dw}= \\ $$$$=−\frac{\mathrm{5}}{\mathrm{2sinx}}\:+\:\frac{\mathrm{1}}{\mathrm{cosx}}\:+\:\mathrm{C} \\ $$$$\Rightarrow\mathrm{I}=\int\frac{\mathrm{5cos}^{\mathrm{3}} \mathrm{x}+\mathrm{2sin}^{\mathrm{3}} \mathrm{x}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{xcos}^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{cosx}}−\frac{\mathrm{5}}{\mathrm{2sinx}}+\mathrm{C} \\ $$

Commented by mondodotto@gmail.com last updated on 09/Jul/17

$$\mathrm{thanx}\:\:\mathrm{really}\:\mathrm{appreciated}\:\mathrm{sir} \\ $$

Answered by Arnab Maiti last updated on 11/Jul/17

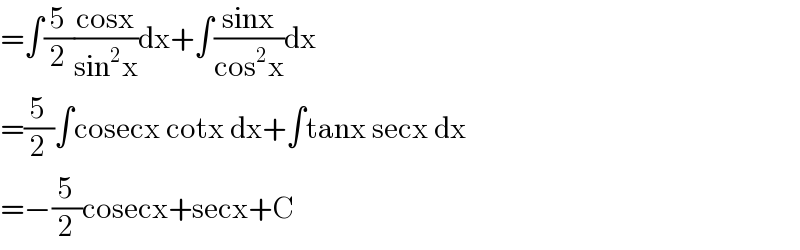
=∫(5/2)((cosx)/(sin^2 x))dx+∫((sinx)/(cos^2 x))dx =(5/2)∫cosecx cotx dx+∫tanx secx dx =−(5/2)cosecx+secx+C

$$=\int\frac{\mathrm{5}}{\mathrm{2}}\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}+\int\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\mathrm{cosecx}\:\mathrm{cotx}\:\mathrm{dx}+\int\mathrm{tanx}\:\mathrm{secx}\:\mathrm{dx} \\ $$$$=−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{cosecx}+\mathrm{secx}+\mathrm{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply