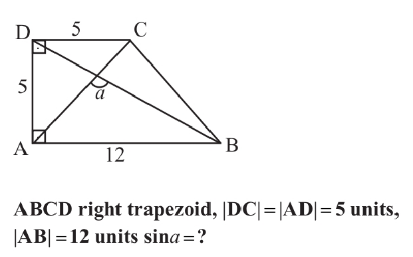
Question Number 176816 by Ar Brandon last updated on 27/Sep/22
Commented by MJS_new last updated on 27/Sep/22
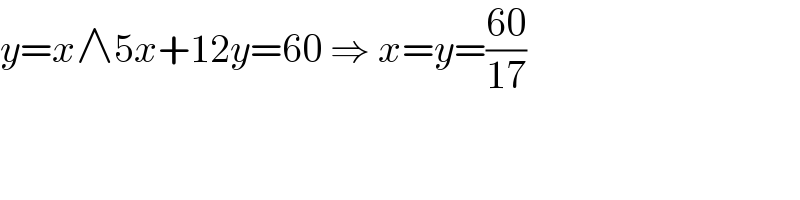
$${y}={x}\wedge\mathrm{5}{x}+\mathrm{12}{y}=\mathrm{60}\:\Rightarrow\:{x}={y}=\frac{\mathrm{60}}{\mathrm{17}} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Oh! Thank you Sir MJS
Commented by cortano1 last updated on 27/Sep/22
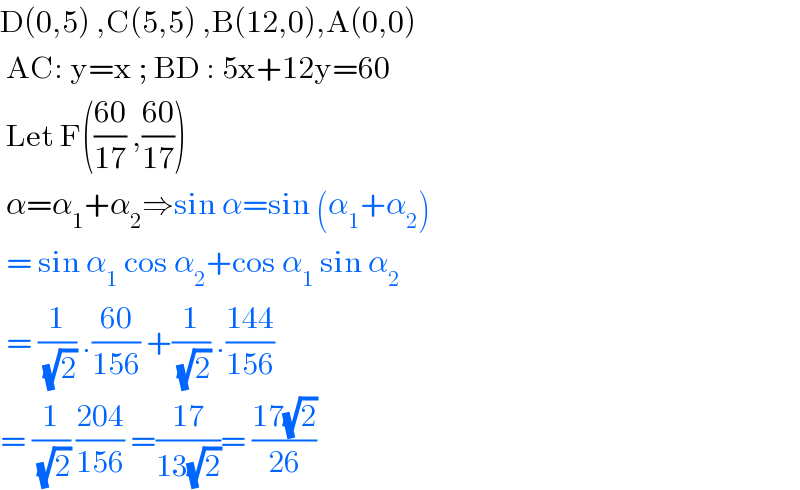
$$\mathrm{D}\left(\mathrm{0},\mathrm{5}\right)\:,\mathrm{C}\left(\mathrm{5},\mathrm{5}\right)\:,\mathrm{B}\left(\mathrm{12},\mathrm{0}\right),\mathrm{A}\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\:\mathrm{AC}:\:\mathrm{y}=\mathrm{x}\:;\:\mathrm{BD}\::\:\mathrm{5x}+\mathrm{12y}=\mathrm{60} \\ $$$$\:\mathrm{Let}\:\mathrm{F}\left(\frac{\mathrm{60}}{\mathrm{17}}\:,\frac{\mathrm{60}}{\mathrm{17}}\right) \\ $$$$\:\alpha=\alpha_{\mathrm{1}} +\alpha_{\mathrm{2}} \Rightarrow\mathrm{sin}\:\alpha=\mathrm{sin}\:\left(\alpha_{\mathrm{1}} +\alpha_{\mathrm{2}} \right) \\ $$$$\:=\:\mathrm{sin}\:\alpha_{\mathrm{1}} \:\mathrm{cos}\:\alpha_{\mathrm{2}} +\mathrm{cos}\:\alpha_{\mathrm{1}} \:\mathrm{sin}\:\alpha_{\mathrm{2}} \\ $$$$\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\frac{\mathrm{60}}{\mathrm{156}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\frac{\mathrm{144}}{\mathrm{156}} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\frac{\mathrm{204}}{\mathrm{156}}\:=\frac{\mathrm{17}}{\mathrm{13}\sqrt{\mathrm{2}}}=\:\frac{\mathrm{17}\sqrt{\mathrm{2}}}{\mathrm{26}} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
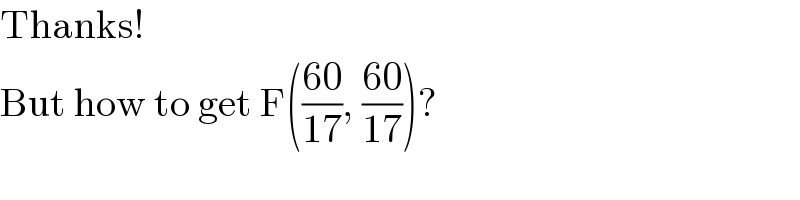
$$\mathrm{Thanks}! \\ $$$$\mathrm{But}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{F}\left(\frac{\mathrm{60}}{\mathrm{17}},\:\frac{\mathrm{60}}{\mathrm{17}}\right)? \\ $$
Answered by mr W last updated on 27/Sep/22
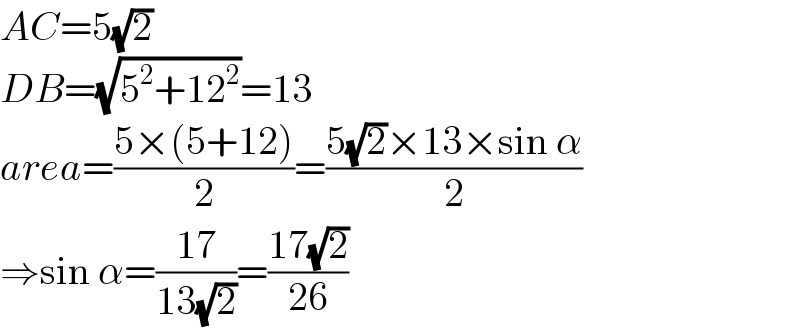
$${AC}=\mathrm{5}\sqrt{\mathrm{2}} \\ $$$${DB}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{13} \\ $$$${area}=\frac{\mathrm{5}×\left(\mathrm{5}+\mathrm{12}\right)}{\mathrm{2}}=\frac{\mathrm{5}\sqrt{\mathrm{2}}×\mathrm{13}×\mathrm{sin}\:\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{17}}{\mathrm{13}\sqrt{\mathrm{2}}}=\frac{\mathrm{17}\sqrt{\mathrm{2}}}{\mathrm{26}} \\ $$
Answered by HeferH last updated on 27/Sep/22
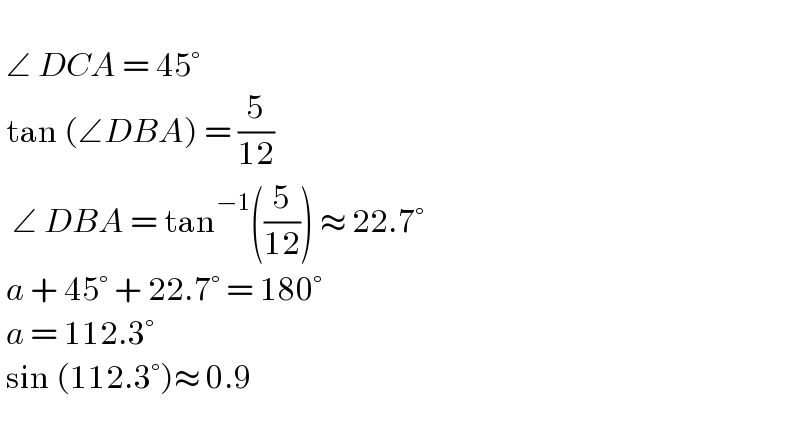
$$\: \\ $$$$\:\angle\:{DCA}\:=\:\mathrm{45}° \\ $$$$\:\mathrm{tan}\:\left(\angle{DBA}\right)\:=\:\frac{\mathrm{5}}{\mathrm{12}}\: \\ $$$$\:\:\angle\:{DBA}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{12}}\right)\:\approx\:\mathrm{22}.\mathrm{7}° \\ $$$$\:{a}\:+\:\mathrm{45}°\:+\:\mathrm{22}.\mathrm{7}°\:=\:\mathrm{180}° \\ $$$$\:{a}\:=\:\mathrm{112}.\mathrm{3}° \\ $$$$\:\mathrm{sin}\:\left(\mathrm{112}.\mathrm{3}°\right)\approx\:\mathrm{0}.\mathrm{9} \\ $$$$\: \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thank you ��
Answered by som(math1967) last updated on 27/Sep/22

$$\angle{DAC}=\angle{DCA}=\frac{\pi}{\mathrm{4}} \\ $$$$\therefore\angle{CAB}=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$$$\:{BD}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{13} \\ $$$$\therefore\angle{ABD}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{13}} \\ $$$$\:{a}=\pi−\frac{\pi}{\mathrm{4}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{13}} \\ $$$${sina}={sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\:−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{13}}\right) \\ $$$$\:={sin}\frac{\mathrm{3}\pi}{\mathrm{4}}{cos}\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{13}}\right)−{cos}\frac{\mathrm{3}\pi}{\mathrm{4}}{sin}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{13}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\mathrm{12}}{\mathrm{13}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\mathrm{5}}{\mathrm{13}}\:\bigstar \\ $$$$=\frac{\mathrm{17}}{\:\mathrm{13}\sqrt{\mathrm{2}}}=\frac{\mathrm{17}\sqrt{\mathrm{2}}}{\mathrm{26}} \\ $$$$\bigstar\:{cos}\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{13}}\right)={cos}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}}\right) \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Great! Thanks!
Commented by Tawa11 last updated on 28/Sep/22

$$\mathrm{Great}\:\mathrm{sirs}. \\ $$
