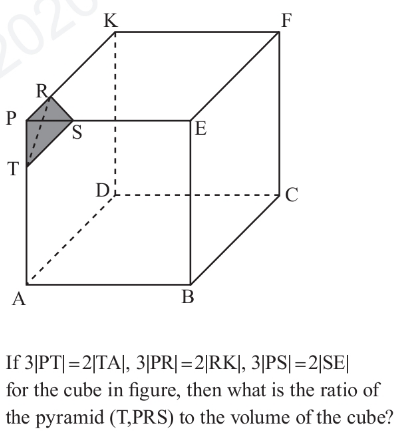
Question Number 176853 by Ar Brandon last updated on 27/Sep/22
Answered by som(math1967) last updated on 27/Sep/22

$$\:\frac{{PT}}{{TA}}=\frac{{PR}}{{RK}}=\frac{{PS}}{{SE}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${let}\:{PT}={PR}={PS}=\mathrm{2}{x}\: \\ $$$${TA}=\mathrm{3}{x} \\ $$$$\therefore\:{each}\:{side}\:{of}\:{cube}={PT}+{TA}=\mathrm{5}{x} \\ $$$$\:{vol}\:{of}\:{pyramid}=\frac{\mathrm{1}}{\mathrm{3}}×{ar}\bigtriangleup{PTS}×{PR} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{x}×\mathrm{2}{x}×\mathrm{2}{x}=\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${vol}\:{of}\:{cube}=\left(\mathrm{5}{x}\right)^{\mathrm{3}} =\mathrm{125}{x}^{\mathrm{3}} \\ $$$$\:{ratio}\:{of}\:{volume}\:{of}\:{them} \\ $$$$\:\:\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{3}}:\mathrm{125}{x}^{\mathrm{3}} \\ $$$$\:\:\mathrm{4}:\mathrm{375} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thank you Sir
Answered by mr W last updated on 27/Sep/22

$$\mathrm{3}×{PT}=\mathrm{2}×{TA}\: \\ $$$$\Rightarrow\frac{{PT}}{{PA}}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${similarly}\: \\ $$$$\Rightarrow\frac{{PR}}{{PK}}=\frac{\mathrm{2}}{\mathrm{5}},\:\frac{{PS}}{{PE}}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${volume}\:{of}\:{pyramid}=\frac{{PT}×{PR}×{PS}}{\mathrm{6}} \\ $$$${volume}\:{of}\:{cube}={PA}×{PK}×{PE} \\ $$$$\frac{{volume}\:{of}\:{pyramid}}{{volume}\:{of}\:{cube}}=\frac{{PT}×{PR}×{PS}}{\mathrm{6}×{PA}×{PK}×{PE}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}×\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{3}} =\frac{\mathrm{4}}{\mathrm{375}} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thank you Sir!
