Question Number 176888 by mr W last updated on 27/Sep/22
Commented by mr W last updated on 27/Sep/22

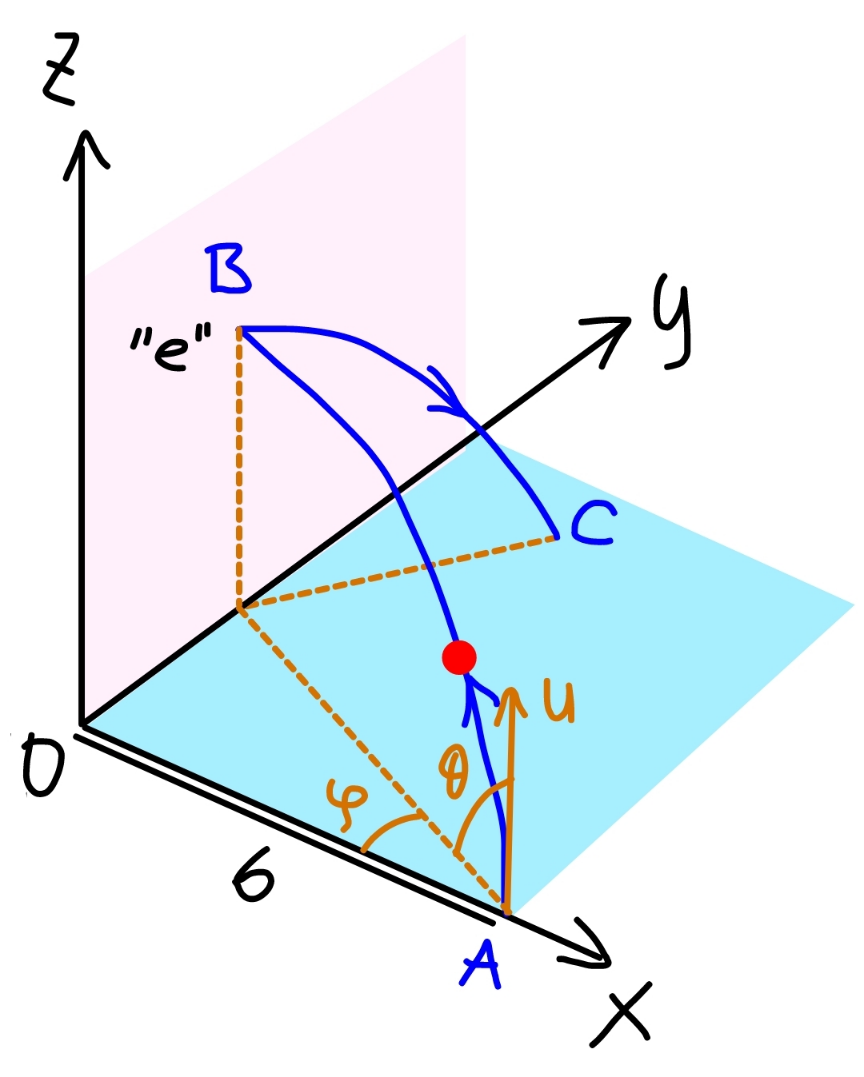
$${a}\:{ball}\:{is}\:{projected}\:{from}\:{point}\:{A}\:{on}\:{the} \\ $$$${ground}\:{against}\:{a}\:{wall}\:{as}\:{shown}\:{and} \\ $$$${hits}\:{the}\:{wall}\:{at}\:{point}\:{B}.\: \\ $$$${if}\:{the}\:{coefficient}\:{of}\:{restitution}\:{is}\:{e}, \\ $$$${find}\:{the}\:{position}\:{of}\:{point}\:{C}\:{where} \\ $$$${the}\:{ball}\:{hits}\:{the}\:{ground}\:{again}. \\ $$$$\left({b},\:{u},\:\theta,\:\varphi,\:{e}\:{are}\:{given}\right) \\ $$
Commented by mr W last updated on 27/Sep/22
$${nice}\:{youtube}\:{video}\:{sir}!\:{i}\:{wish}\:{you} \\ $$$${much}\:{success}\:{with}\:{your}\:{channel}! \\ $$
Commented by ajfour last updated on 27/Sep/22
https://youtu.be/Ix0JqOQR_0g
Answered by mr W last updated on 28/Sep/22
Commented by mr W last updated on 29/Sep/22

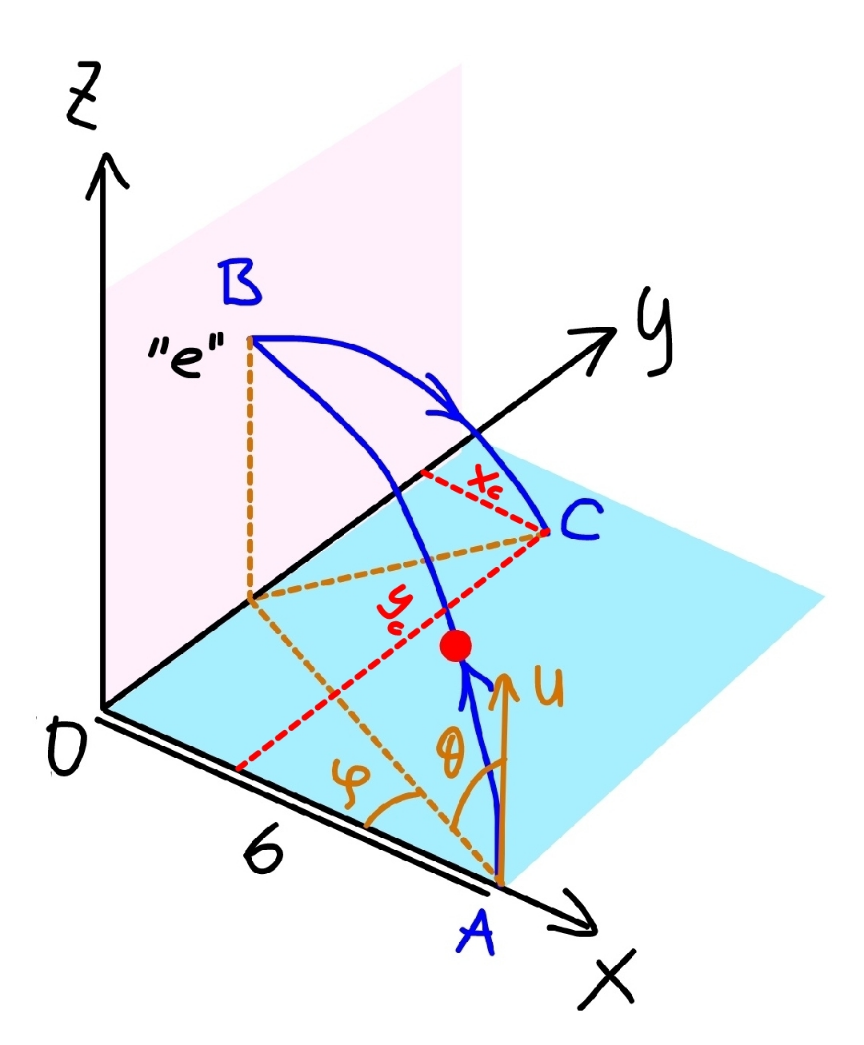
$${the}\:{collision}\:{with}\:{the}\:{wall}\:{doesn}'{t} \\ $$$${affect}\:{the}\:{motion}\:{of}\:{the}\:{ball}\:{in}\:{the} \\ $$$${Y}−\:{and}\:{Z}−{direction}.\: \\ $$$${total}\:{flight}\:{time}\:{of}\:{the}\:{ball}\:{in}\:{the}\:{air} \\ $$$${is}\:{t}=\frac{\mathrm{2}{u}\:\mathrm{sin}\:\theta}{{g}}. \\ $$$${the}\:{distance}\:{the}\:{ball}\:{traveled}\:{in}\:{this} \\ $$$${time}\:{in}\:{Y}−{direction}\:{is} \\ $$$${y}_{{C}} ={u}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi×\frac{\mathrm{2}{u}\:\mathrm{sin}\:\theta}{{g}} \\ $$$$\Rightarrow{y}_{{C}} =\frac{{u}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}\:\varphi}{{g}} \\ $$$${before}\:{the}\:{collision}\:{with}\:{the}\:{wall}\:{the} \\ $$$${ball}\:{moved}\:{in}\:{X}−{direction}\:{with}\:{speed} \\ $$$${v}_{{x},\:{i}} ={u}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi \\ $$$${after}\:{the}\:{collision}\:{its}\:{speed}\: \\ $$$${in}\:{X}−{direction}\:{is} \\ $$$${v}_{{x},\:{f}} ={e}\:{v}_{{x},\:{i}} ={eu}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi \\ $$$$\frac{{b}}{{v}_{{x},\:{i}} }+\frac{{x}_{{C}} }{{v}_{{x},\:{f}} }={t} \\ $$$${x}_{{C}} ={e}\left({tv}_{{x},\:{i}} −{b}\right) \\ $$$${x}_{{C}} ={e}\left(\frac{\mathrm{2}{u}\:\mathrm{sin}\:\theta}{{g}}×{u}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi−{b}\right) \\ $$$$\Rightarrow{x}_{{C}} ={e}\left(\frac{{u}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta\:\mathrm{cos}\:\varphi}{{g}}−{b}\right) \\ $$
Commented by Tawa11 last updated on 03/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
