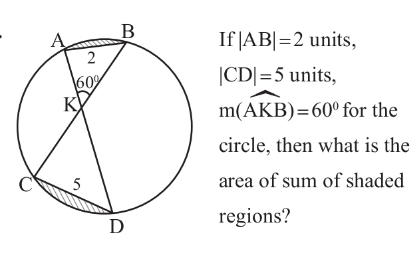
Question Number 176946 by Ar Brandon last updated on 28/Sep/22
Answered by mr W last updated on 29/Sep/22

Commented by mr W last updated on 29/Sep/22
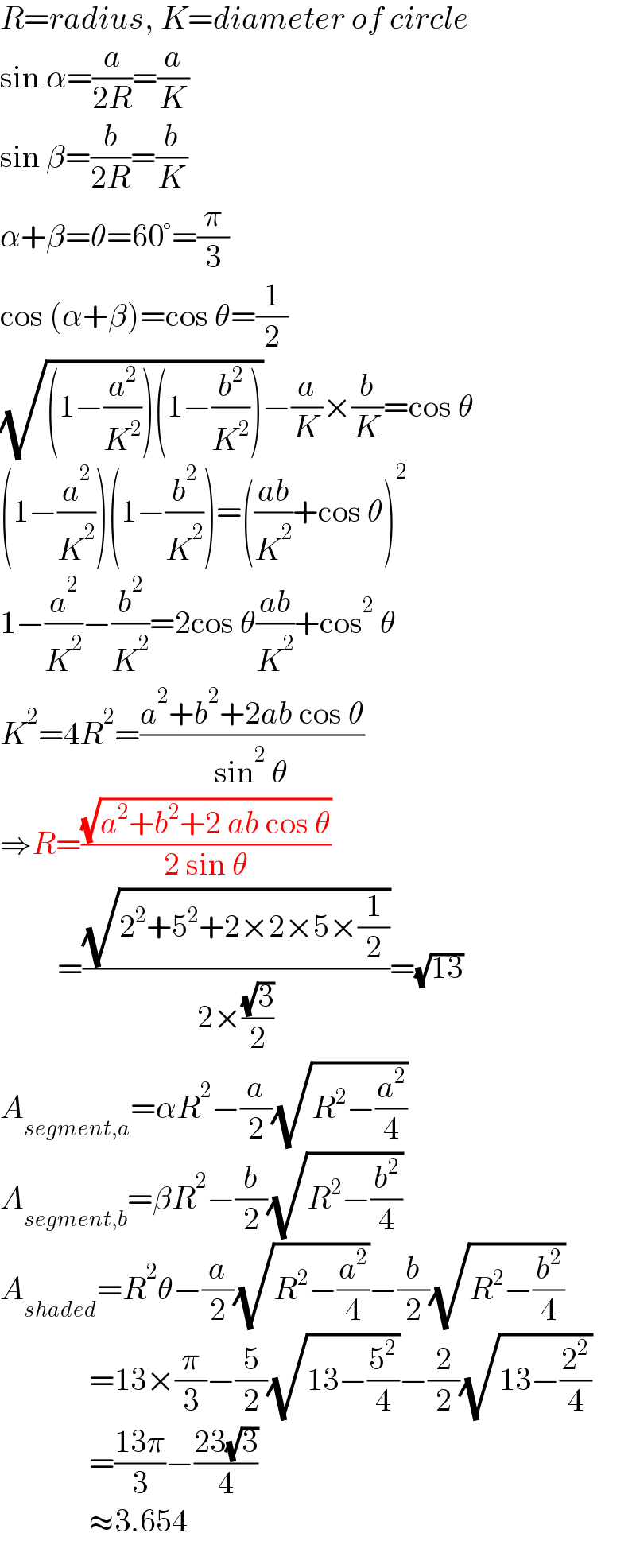
$${R}={radius},\:{K}={diameter}\:{of}\:{circle} \\ $$$$\mathrm{sin}\:\alpha=\frac{{a}}{\mathrm{2}{R}}=\frac{{a}}{{K}} \\ $$$$\mathrm{sin}\:\beta=\frac{{b}}{\mathrm{2}{R}}=\frac{{b}}{{K}} \\ $$$$\alpha+\beta=\theta=\mathrm{60}°=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\sqrt{\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{K}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{K}^{\mathrm{2}} }\right)}−\frac{{a}}{{K}}×\frac{{b}}{{K}}=\mathrm{cos}\:\theta \\ $$$$\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{K}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{K}^{\mathrm{2}} }\right)=\left(\frac{{ab}}{{K}^{\mathrm{2}} }+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{K}^{\mathrm{2}} }−\frac{{b}^{\mathrm{2}} }{{K}^{\mathrm{2}} }=\mathrm{2cos}\:\theta\frac{{ab}}{{K}^{\mathrm{2}} }+\mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$${K}^{\mathrm{2}} =\mathrm{4}{R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\theta}{\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{R}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\:{ab}\:\mathrm{cos}\:\theta}}{\mathrm{2}\:\mathrm{sin}\:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\mathrm{2}×\mathrm{2}×\mathrm{5}×\frac{\mathrm{1}}{\mathrm{2}}}}{\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\sqrt{\mathrm{13}} \\ $$$${A}_{{segment},{a}} =\alpha{R}^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${A}_{{segment},{b}} =\beta{R}^{\mathrm{2}} −\frac{{b}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${A}_{{shaded}} ={R}^{\mathrm{2}} \theta−\frac{{a}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}−\frac{{b}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{13}×\frac{\pi}{\mathrm{3}}−\frac{\mathrm{5}}{\mathrm{2}}\sqrt{\mathrm{13}−\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{4}}}−\frac{\mathrm{2}}{\mathrm{2}}\sqrt{\mathrm{13}−\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{13}\pi}{\mathrm{3}}−\frac{\mathrm{23}\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{3}.\mathrm{654} \\ $$
Commented by Ar Brandon last updated on 29/Sep/22
Thank you, Sir!
Commented by Tawa11 last updated on 02/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
