Question Number 176950 by cortano1 last updated on 28/Sep/22

Answered by mr W last updated on 28/Sep/22
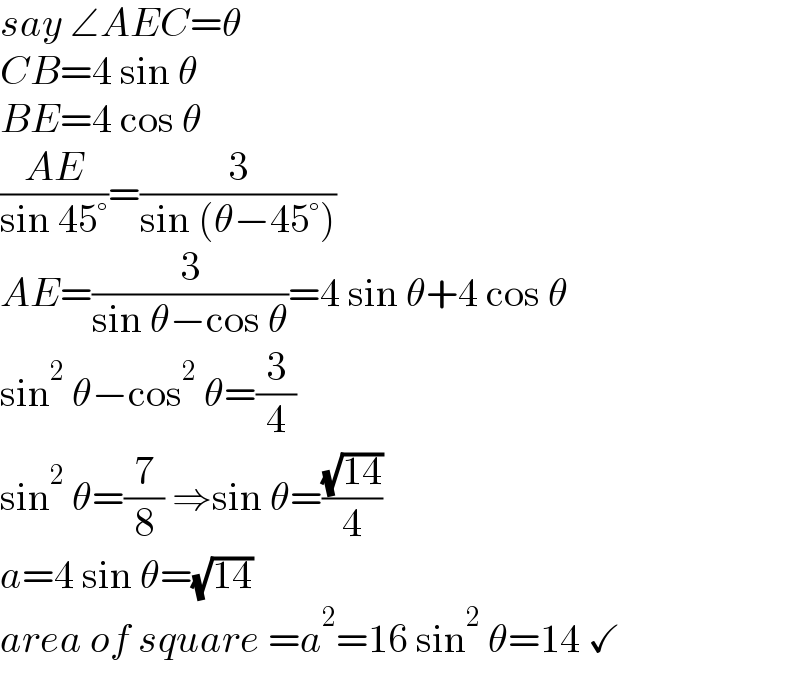
$${say}\:\angle{AEC}=\theta \\ $$$${CB}=\mathrm{4}\:\mathrm{sin}\:\theta \\ $$$${BE}=\mathrm{4}\:\mathrm{cos}\:\theta \\ $$$$\frac{{AE}}{\mathrm{sin}\:\mathrm{45}°}=\frac{\mathrm{3}}{\mathrm{sin}\:\left(\theta−\mathrm{45}°\right)} \\ $$$${AE}=\frac{\mathrm{3}}{\mathrm{sin}\:\theta−\mathrm{cos}\:\theta}=\mathrm{4}\:\mathrm{sin}\:\theta+\mathrm{4}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{cos}^{\mathrm{2}} \:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta=\frac{\mathrm{7}}{\mathrm{8}}\:\Rightarrow\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{14}}}{\mathrm{4}} \\ $$$${a}=\mathrm{4}\:\mathrm{sin}\:\theta=\sqrt{\mathrm{14}} \\ $$$${area}\:{of}\:{square}\:={a}^{\mathrm{2}} =\mathrm{16}\:\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{14}\:\checkmark \\ $$
Commented by Tawa11 last updated on 28/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by cortano1 last updated on 29/Sep/22

$$\mathrm{nice} \\ $$
