Question Number 176963 by Ml last updated on 28/Sep/22

Commented by Frix last updated on 29/Sep/22
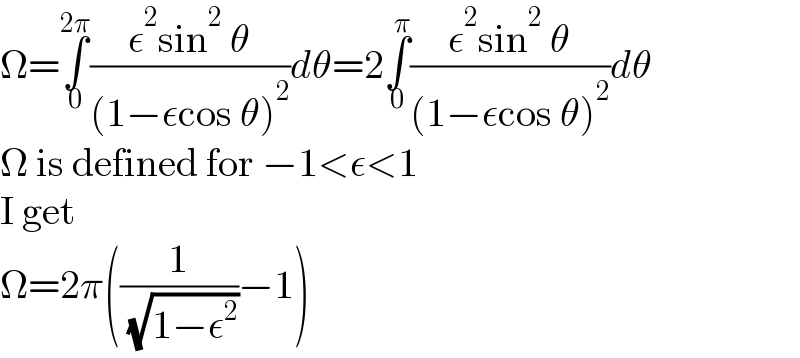
$$\Omega=\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\frac{\epsilon^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}−\epsilon\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{d}\theta=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\epsilon^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}−\epsilon\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$\Omega\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:−\mathrm{1}<\epsilon<\mathrm{1} \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$$\Omega=\mathrm{2}\pi\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\epsilon^{\mathrm{2}} }}−\mathrm{1}\right) \\ $$
Answered by Ar Brandon last updated on 28/Sep/22
![I=∫_0 ^(2π) ((ξ^2 sin^2 ϑ)/((1−ξcosϑ)^2 ))dϑ =∫_0 ^(2π) ((ξsinϑ)/((1−ξcosϑ)^2 ))∙ξsinϑdϑ =[−((ξsinϑ)/(1−ξcosϑ))]_0 ^(2π) +∫_0 ^(2π) ((ξcosϑ)/(1−ξcosϑ))dϑ =∫_0 ^(2π) ((1/(1−ξcosϑ))−1)dϑ=∫_0 ^(2π) (1/(1−ξcosϑ))−2π J=∫(1/(1−ξcosϑ))dϑ=∫(1/(1−ξ(((1−t^2 )/(1+t^2 )))))∙(2/(1+t^2 ))dt, t=tan(ϑ/2) =∫(2/(1+t^2 −ξ(1+t^2 )))dt=∫(2/((1−ξ)t^2 +(1−ξ)))dt =(2/(1−ξ))∫(1/(t^2 +1))dt=(2/(1−ξ))(arctan(t))+C =(2/(1−ξ))(arctan(tan((ϑ/2))))+C](https://www.tinkutara.com/question/Q176970.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\xi^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \vartheta}{\left(\mathrm{1}−\xi\mathrm{cos}\vartheta\right)^{\mathrm{2}} }{d}\vartheta \\ $$$$\:\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\xi\mathrm{sin}\vartheta}{\left(\mathrm{1}−\xi\mathrm{cos}\vartheta\right)^{\mathrm{2}} }\centerdot\xi\mathrm{sin}\vartheta{d}\vartheta \\ $$$$\:\:=\left[−\frac{\xi\mathrm{sin}\vartheta}{\mathrm{1}−\xi\mathrm{cos}\vartheta}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} +\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\xi\mathrm{cos}\vartheta}{\mathrm{1}−\xi\mathrm{cos}\vartheta}{d}\vartheta \\ $$$$\:\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\frac{\mathrm{1}}{\mathrm{1}−\xi\mathrm{cos}\vartheta}−\mathrm{1}\right){d}\vartheta=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\mathrm{1}−\xi\mathrm{cos}\vartheta}−\mathrm{2}\pi \\ $$$${J}=\int\frac{\mathrm{1}}{\mathrm{1}−\xi\mathrm{cos}\vartheta}{d}\vartheta=\int\frac{\mathrm{1}}{\mathrm{1}−\xi\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\centerdot\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt},\:{t}=\mathrm{tan}\frac{\vartheta}{\mathrm{2}} \\ $$$$\:\:\:=\int\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} −\xi\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}=\int\frac{\mathrm{2}}{\left(\mathrm{1}−\xi\right){t}^{\mathrm{2}} +\left(\mathrm{1}−\xi\right)}{dt} \\ $$$$\:\:\:=\frac{\mathrm{2}}{\mathrm{1}−\xi}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\mathrm{2}}{\mathrm{1}−\xi}\left(\mathrm{arctan}\left({t}\right)\right)+{C} \\ $$$$\:\:\:=\frac{\mathrm{2}}{\mathrm{1}−\xi}\left(\mathrm{arctan}\left(\mathrm{tan}\left(\frac{\vartheta}{\mathrm{2}}\right)\right)\right)+{C} \\ $$
