Question-176991

Question Number 176991 by mathlove last updated on 29/Sep/22

Answered by som(math1967) last updated on 29/Sep/22

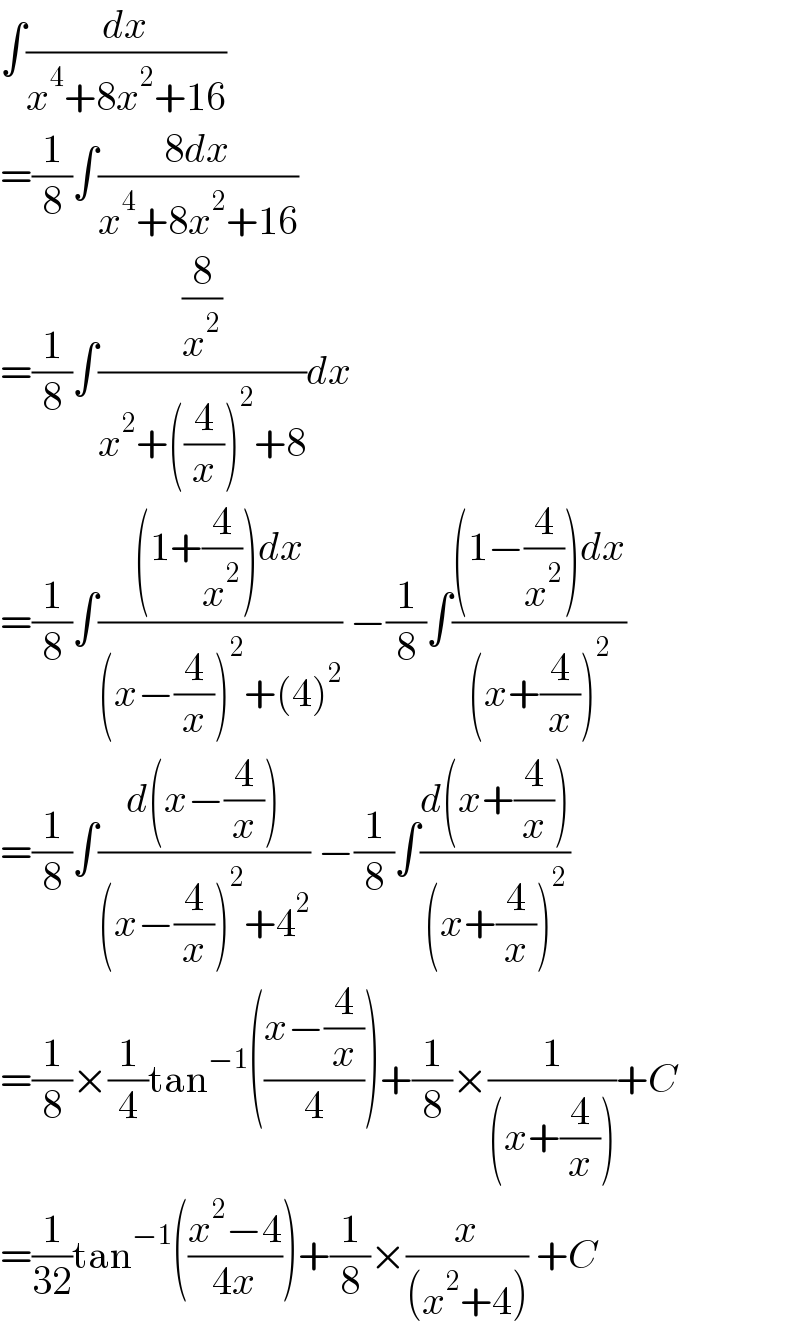
∫(dx/(x^4 +8x^2 +16)) =(1/8)∫((8dx)/(x^4 +8x^2 +16)) =(1/8)∫((8/x^2 )/(x^2 +((4/x))^2 +8))dx =(1/8)∫(((1+(4/x^2 ))dx)/((x−(4/x))^2 +(4)^2 )) −(1/8)∫(((1−(4/x^2 ))dx)/((x+(4/x))^2 )) =(1/8)∫((d(x−(4/x)))/((x−(4/x))^2 +4^2 )) −(1/8)∫((d(x+(4/x)))/((x+(4/x))^2 )) =(1/8)×(1/4)tan^(−1) (((x−(4/x))/4))+(1/8)×(1/((x+(4/x))))+C =(1/(32))tan^(−1) (((x^2 −4)/(4x)))+(1/8)×(x/((x^2 +4))) +C

$$\int\frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{8}{dx}}{{x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\frac{\mathrm{8}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\left(\frac{\mathrm{4}}{{x}}\right)^{\mathrm{2}} +\mathrm{8}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right){dx}}{\left({x}−\frac{\mathrm{4}}{{x}}\right)^{\mathrm{2}} +\left(\mathrm{4}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\left(\mathrm{1}−\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right){dx}}{\left({x}+\frac{\mathrm{4}}{{x}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{d}\left({x}−\frac{\mathrm{4}}{{x}}\right)}{\left({x}−\frac{\mathrm{4}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{d}\left({x}+\frac{\mathrm{4}}{{x}}\right)}{\left({x}+\frac{\mathrm{4}}{{x}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{4}}{{x}}}{\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{4}}{{x}}\right)}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}{x}}\right)+\frac{\mathrm{1}}{\mathrm{8}}×\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)}\:+{C} \\ $$

Commented by mathlove last updated on 29/Sep/22

$${thanks} \\ $$

Commented by peter frank last updated on 29/Sep/22

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by Mathspace last updated on 29/Sep/22

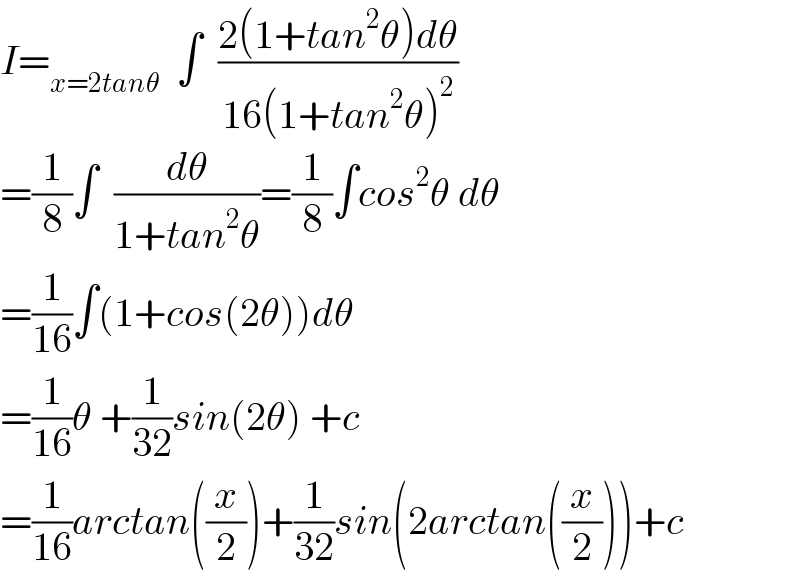
I=_(x=2tanθ) ∫ ((2(1+tan^2 θ)dθ)/(16(1+tan^2 θ)^2 )) =(1/8)∫ (dθ/(1+tan^2 θ))=(1/8)∫cos^2 θ dθ =(1/(16))∫(1+cos(2θ))dθ =(1/(16))θ +(1/(32))sin(2θ) +c =(1/(16))arctan((x/2))+(1/(32))sin(2arctan((x/2)))+c

$${I}=_{{x}=\mathrm{2}{tan}\theta} \:\:\int\:\:\frac{\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\mathrm{16}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}=\frac{\mathrm{1}}{\mathrm{8}}\int{cos}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\int\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\theta\:+\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{2}\theta\right)\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}{arctan}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{2}{arctan}\left(\frac{{x}}{\mathrm{2}}\right)\right)+{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply