Menu Close

Question-177031

Tinku Tara 0 Comments
Pin




Question Number 177031 by HeferH last updated on 29/Sep/22
Answered by mr W last updated on 30/Sep/22
Commented by mr W last updated on 30/Sep/22
cos^(−1) (5/(2R))−cos^(−1) (6/(2R))=30° (5/(2R))×(6/(2R))+(√((1−((25)/(4R^2 )))(1−((36)/(4R^2 )))))=((√3)/2) (1−((25)/(4R^2 )))(1−((36)/(4R^2 )))=(((√3)/2)−((30)/(4R^2 )))^2 1−((61)/(4R^2 ))+((25×36)/((4R^2 )^2 ))=(3/4)−((30(√3))/(4R^2 ))+((30^2 )/((4R^2 )^2 )) ((61−30(√3))/R^2 )=1 ⇒R=(√(61−30(√3))) CD=(√(R^2 −((5/2))^2 ))=(√(61−30(√3)−((25)/4)))=((√(219−120(√3)))/2) CB=R−r DE=(r/(tan 15°))−(5/2)=(2+(√3))r−(5/2) CD−BE=((√(219−120(√3)))/2)−r (((√(219−120(√3)))/2)−r)^2 +((2+(√3))r−(5/2))^2 =((√(61−30(√3)))−r)^2 ((219−120(√3))/4)−(√(219−120(√3)))r+(2+(√3))^2 r^2 −5(2+(√3))r+((25)/4)=61−30(√3)−2(√(61−30(√3)))r (2+(√3))^2 r=(√(219−120(√3)))+5(2+(√3))−2(√(61−30(√3))) ⇒r=(((√(219−120(√3)))+5(2+(√3))−2(√(61−30(√3))))/((2+(√3))^2 )) ≈1.147828
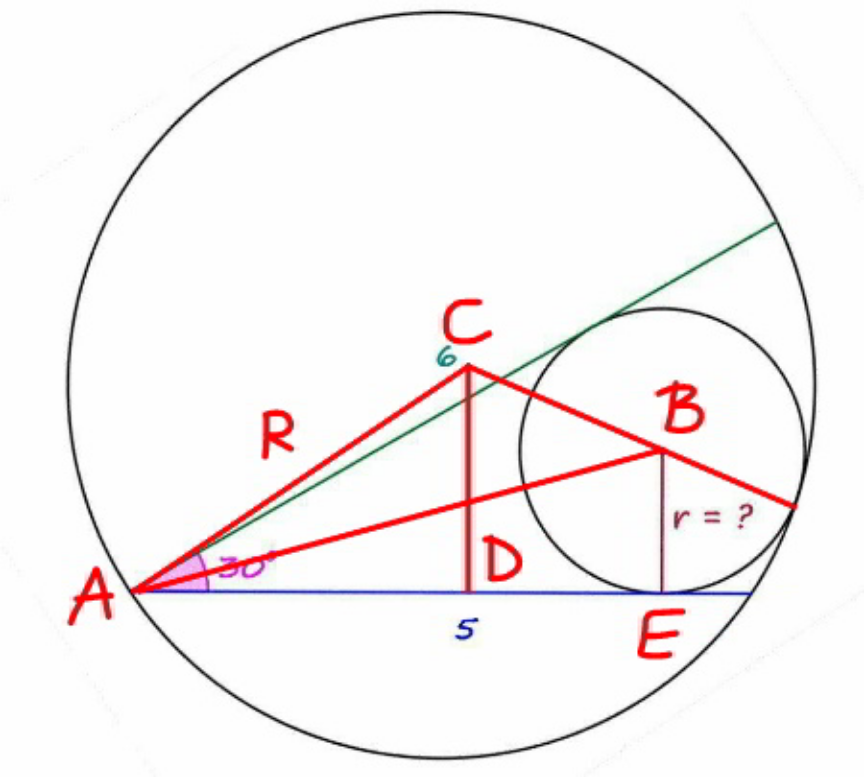
$$\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{2}{R}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{6}}{\mathrm{2}{R}}=\mathrm{30}° \\ $$$$\frac{\mathrm{5}}{\mathrm{2}{R}}×\frac{\mathrm{6}}{\mathrm{2}{R}}+\sqrt{\left(\mathrm{1}−\frac{\mathrm{25}}{\mathrm{4}{R}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{36}}{\mathrm{4}{R}^{\mathrm{2}} }\right)}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{25}}{\mathrm{4}{R}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{36}}{\mathrm{4}{R}^{\mathrm{2}} }\right)=\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{30}}{\mathrm{4}{R}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\mathrm{1}−\frac{\mathrm{61}}{\mathrm{4}{R}^{\mathrm{2}} }+\frac{\mathrm{25}×\mathrm{36}}{\left(\mathrm{4}{R}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{30}\sqrt{\mathrm{3}}}{\mathrm{4}{R}^{\mathrm{2}} }+\frac{\mathrm{30}^{\mathrm{2}} }{\left(\mathrm{4}{R}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}{{R}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{R}=\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}} \\ $$$${CD}=\sqrt{{R}^{\mathrm{2}} −\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}−\frac{\mathrm{25}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$${CB}={R}−{r} \\ $$$${DE}=\frac{{r}}{\mathrm{tan}\:\mathrm{15}°}−\frac{\mathrm{5}}{\mathrm{2}}=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){r}−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${CD}−{BE}=\frac{\sqrt{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}}{\mathrm{2}}−{r} \\ $$$$\left(\frac{\sqrt{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}}{\mathrm{2}}−{r}\right)^{\mathrm{2}} +\left(\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){r}−\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}−{r}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}{\mathrm{4}}−\sqrt{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}{r}+\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{5}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){r}+\frac{\mathrm{25}}{\mathrm{4}}=\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}{r} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} {r}=\sqrt{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}+\mathrm{5}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)−\mathrm{2}\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{219}−\mathrm{120}\sqrt{\mathrm{3}}}+\mathrm{5}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)−\mathrm{2}\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}}}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\approx\mathrm{1}.\mathrm{147828} \\ $$
Commented by mr W last updated on 30/Sep/22
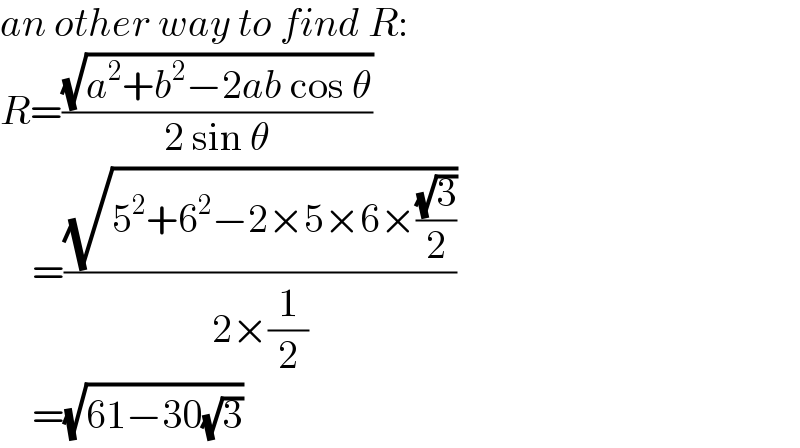
an other way to find R: R=((√(a^2 +b^2 −2ab cos θ))/(2 sin θ)) =((√(5^2 +6^2 −2×5×6×((√3)/2)))/(2×(1/2))) =(√(61−30(√3)))
$${an}\:{other}\:{way}\:{to}\:{find}\:{R}: \\ $$$${R}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\theta}}{\mathrm{2}\:\mathrm{sin}\:\theta} \\ $$$$\:\:\:\:=\frac{\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{2}×\mathrm{5}×\mathrm{6}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:=\sqrt{\mathrm{61}−\mathrm{30}\sqrt{\mathrm{3}}} \\ $$
Commented by Tawa11 last updated on 02/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *