Question Number 177037 by mr W last updated on 30/Sep/22
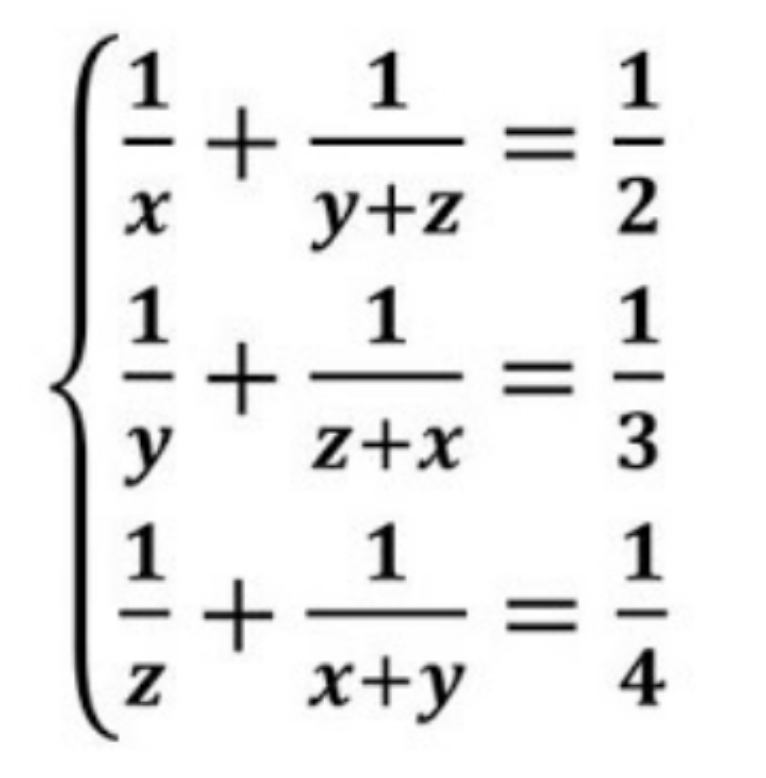
Answered by Rasheed.Sindhi last updated on 30/Sep/22

$$\begin{cases}{\frac{{x}+{y}+{z}}{{x}\left({y}+{z}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{x}+{y}+{z}=\frac{{x}\left({y}+{z}\right)}{\mathrm{2}}}\\{\frac{{x}+{y}+{z}}{{y}\left({z}+{x}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{x}+{y}+{z}=\frac{{y}\left({z}+{x}\right)}{\mathrm{3}}}\\{\frac{{x}+{y}+{z}}{{z}\left({x}+{y}\right)}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow{x}+{y}+{z}=\frac{{z}\left({x}+{y}\right)}{\mathrm{4}}}\end{cases}\: \\ $$$$\begin{cases}{\frac{{x}\left({y}+{z}\right)}{\mathrm{2}}=\frac{{y}\left({z}+{x}\right)}{\mathrm{3}}\Rightarrow\mathrm{3}{xy}+\mathrm{3}{zx}=\mathrm{2}{yz}+\mathrm{2}{xy}}\\{\frac{{y}\left({z}+{x}\right)}{\mathrm{3}}=\frac{{z}\left({x}+{y}\right)}{\mathrm{4}}\Rightarrow\mathrm{4}{yz}+\mathrm{4}{xy}=\mathrm{3}{zx}+\mathrm{3}{yz}\:\:}\\{\frac{{z}\left({x}+{y}\right)}{\mathrm{4}}=\frac{{x}\left({y}+{z}\right)}{\mathrm{2}}\Rightarrow\mathrm{4}{xy}+\mathrm{4}{zx}=\mathrm{2}{zx}+\mathrm{2}{yz}}\end{cases}\:\: \\ $$$$\Rightarrow\begin{cases}{\mathrm{3}{xy}+\mathrm{3}{zx}=\mathrm{2}{yz}+\mathrm{2}{xy}}\\{\mathrm{4}{yz}+\mathrm{4}{xy}=\mathrm{3}{zx}+\mathrm{3}{yz}}\\{\mathrm{4}{xy}+\mathrm{4}{zx}=\mathrm{2}{zx}+\mathrm{2}{yz}}\end{cases}\: \\ $$$$\Rightarrow\begin{cases}{{xy}−\mathrm{2}{yz}+\mathrm{3}{zx}=\mathrm{0}}\\{\mathrm{4}{xy}+{yz}−\mathrm{3}{zx}=\mathrm{0}}\\{\mathrm{4}{xy}−\mathrm{2}{yz}+\mathrm{2}{zx}=\mathrm{0}}\end{cases}\: \\ $$$${Let}\:\:\:\:\:{xy}={a},\:{yz}={b},\:{zx}={c} \\ $$$$\Rightarrow\begin{cases}{{a}−\mathrm{2}{b}+\mathrm{3}{c}=\mathrm{0}…\left({i}\right)}\\{\mathrm{4}{a}+{b}−\mathrm{3}{c}=\mathrm{0}…\left({ii}\right)}\\{\mathrm{4}{a}−\mathrm{2}{b}+\mathrm{2}{c}=\mathrm{0}…\left({iii}\right)}\end{cases}\:\: \\ $$$$\left({i}\right)+\left({ii}\right):\:\mathrm{5}{a}−{b}=\mathrm{0}\Rightarrow{b}=\mathrm{5}{a} \\ $$$$\left({ii}\right)−\left({iii}\right):\mathrm{3}{b}−\mathrm{5}{c}=\mathrm{0}\Rightarrow\mathrm{3}\left(\mathrm{5}{a}\right)=\mathrm{5}{c}\Rightarrow{c}=\mathrm{3}{a} \\ $$$$\mathrm{5}{a}={b}\Rightarrow\mathrm{5}{xy}={yz}\Rightarrow{z}=\mathrm{5}{x};\:{y}\neq\mathrm{0} \\ $$$$\mathrm{3}{a}={c}\Rightarrow\mathrm{3}{xy}={zx}\Rightarrow{z}=\mathrm{3}{y};\:{x}\neq\mathrm{0} \\ $$$$\mathrm{5}{x}=\mathrm{3}{y}\Rightarrow{y}=\frac{\mathrm{5}}{\mathrm{3}}{x},{z}=\mathrm{5}{x} \\ $$$${put}\:{these}\:{values}\:{of}\:{y}\:\&\:{z}\:{in}\:{first} \\ $$$${given}\:{equation}\:{to}\:{get}: \\ $$$${x}=\frac{\mathrm{23}}{\mathrm{10}},{y}=\frac{\mathrm{23}}{\mathrm{6}},{z}=\frac{\mathrm{23}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 30/Sep/22

$${thanks}\:{alot}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 30/Sep/22

$$\boldsymbol{{Sir}}\:\boldsymbol{{mr}}\:\boldsymbol{{W}},\:{what}\:\:{should}\:{we}\:{understand} \\ $$$$\:{by}\:{the}\:{following}\:{situation}? \\ $$$$\Rightarrow\begin{cases}{{a}−\mathrm{2}{b}+\mathrm{3}{c}=\mathrm{0}}\\{\mathrm{4}{a}+{b}−\mathrm{3}{c}=\mathrm{0}}\\{\mathrm{4}{a}−\mathrm{2}{b}+\mathrm{2}{c}=\mathrm{0}}\end{cases}\: \\ $$$$\begin{vmatrix}{\mathrm{1}}&{−\mathrm{2}}&{\:\:\:\:\mathrm{3}}\\{\mathrm{4}}&{\:\:\:\:\:\mathrm{1}}&{−\mathrm{3}}\\{\mathrm{4}}&{−\mathrm{2}}&{\:\:\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{0}\:\: \\ $$$$\mathcal{T}{he}\:{matrix}\:{of}\:{coefficients}\:{is}\:{singular} \\ $$$$\mathcal{D}{oesn}'{t}\:{this}\:{mean}\:{that}\:{the}\:{equation} \\ $$$${has}\:{no}\:{unique}\:{solution}?\:{But}\:{we}\:{can} \\ $$$${see}\:{that}\:{above}\:{has}\:{unique}\:{solution}! \\ $$
Commented by Frix last updated on 30/Sep/22

$${a},\:{b},\:{c}\:\mathrm{are}\:\mathrm{not}\:\mathrm{independent}\:\mathrm{variables} \\ $$
Commented by mr W last updated on 30/Sep/22
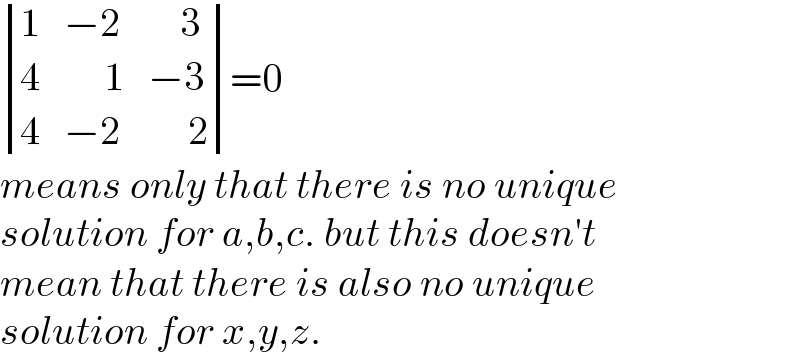
$$\begin{vmatrix}{\mathrm{1}}&{−\mathrm{2}}&{\:\:\:\:\mathrm{3}}\\{\mathrm{4}}&{\:\:\:\:\:\mathrm{1}}&{−\mathrm{3}}\\{\mathrm{4}}&{−\mathrm{2}}&{\:\:\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{0}\:\: \\ $$$${means}\:{only}\:{that}\:{there}\:{is}\:{no}\:{unique} \\ $$$${solution}\:{for}\:{a},{b},{c}.\:{but}\:{this}\:{doesn}'{t} \\ $$$${mean}\:{that}\:{there}\:{is}\:{also}\:{no}\:{unique}\: \\ $$$${solution}\:{for}\:{x},{y},{z}. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Sep/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\:\mathrm{you}\:\boldsymbol{\mathrm{sirs}}! \\ $$
Commented by Rasheed.Sindhi last updated on 30/Sep/22
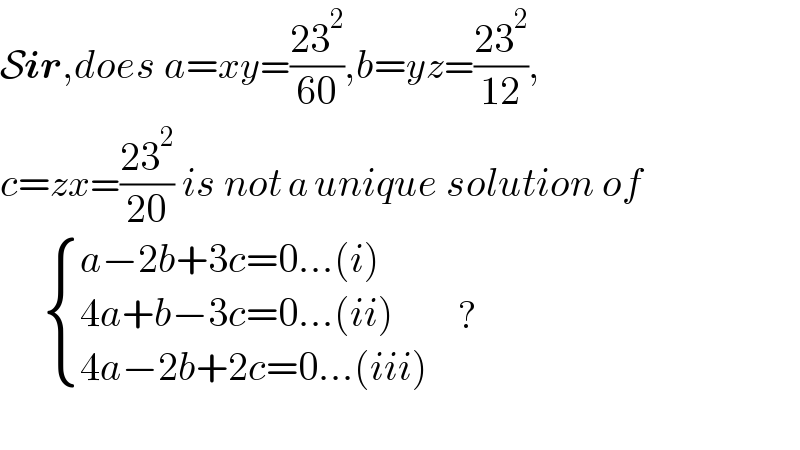
$$\mathcal{S}\boldsymbol{{ir}},{does}\:{a}={xy}=\frac{\mathrm{23}^{\mathrm{2}} }{\mathrm{60}},{b}={yz}=\frac{\mathrm{23}^{\mathrm{2}} }{\mathrm{12}}, \\ $$$${c}={zx}=\frac{\mathrm{23}^{\mathrm{2}} }{\mathrm{20}}\:{is}\:{not}\:{a}\:{unique}\:{solution}\:{of} \\ $$$$\:\:\:\:\:\:\:\begin{cases}{{a}−\mathrm{2}{b}+\mathrm{3}{c}=\mathrm{0}…\left({i}\right)}\\{\mathrm{4}{a}+{b}−\mathrm{3}{c}=\mathrm{0}…\left({ii}\right)}\\{\mathrm{4}{a}−\mathrm{2}{b}+\mathrm{2}{c}=\mathrm{0}…\left({iii}\right)}\end{cases}\:\:\:\:\:? \\ $$$$ \\ $$
Commented by Frix last updated on 30/Sep/22
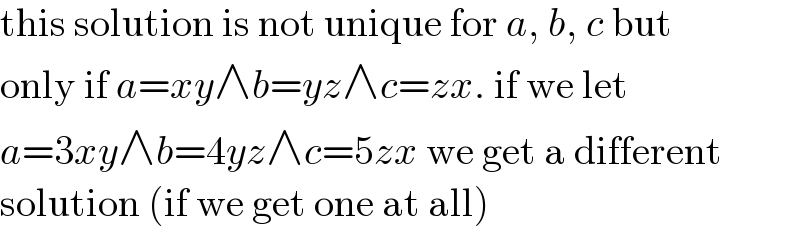
$$\mathrm{this}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique}\:\mathrm{for}\:{a},\:{b},\:{c}\:\mathrm{but} \\ $$$$\mathrm{only}\:\mathrm{if}\:{a}={xy}\wedge{b}={yz}\wedge{c}={zx}.\:\mathrm{if}\:\mathrm{we}\:\mathrm{let} \\ $$$${a}=\mathrm{3}{xy}\wedge{b}=\mathrm{4}{yz}\wedge{c}=\mathrm{5}{zx}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{different} \\ $$$$\mathrm{solution}\:\left(\mathrm{if}\:\mathrm{we}\:\mathrm{get}\:\mathrm{one}\:\mathrm{at}\:\mathrm{all}\right) \\ $$
Commented by Tawa11 last updated on 02/Oct/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by mr W last updated on 30/Sep/22
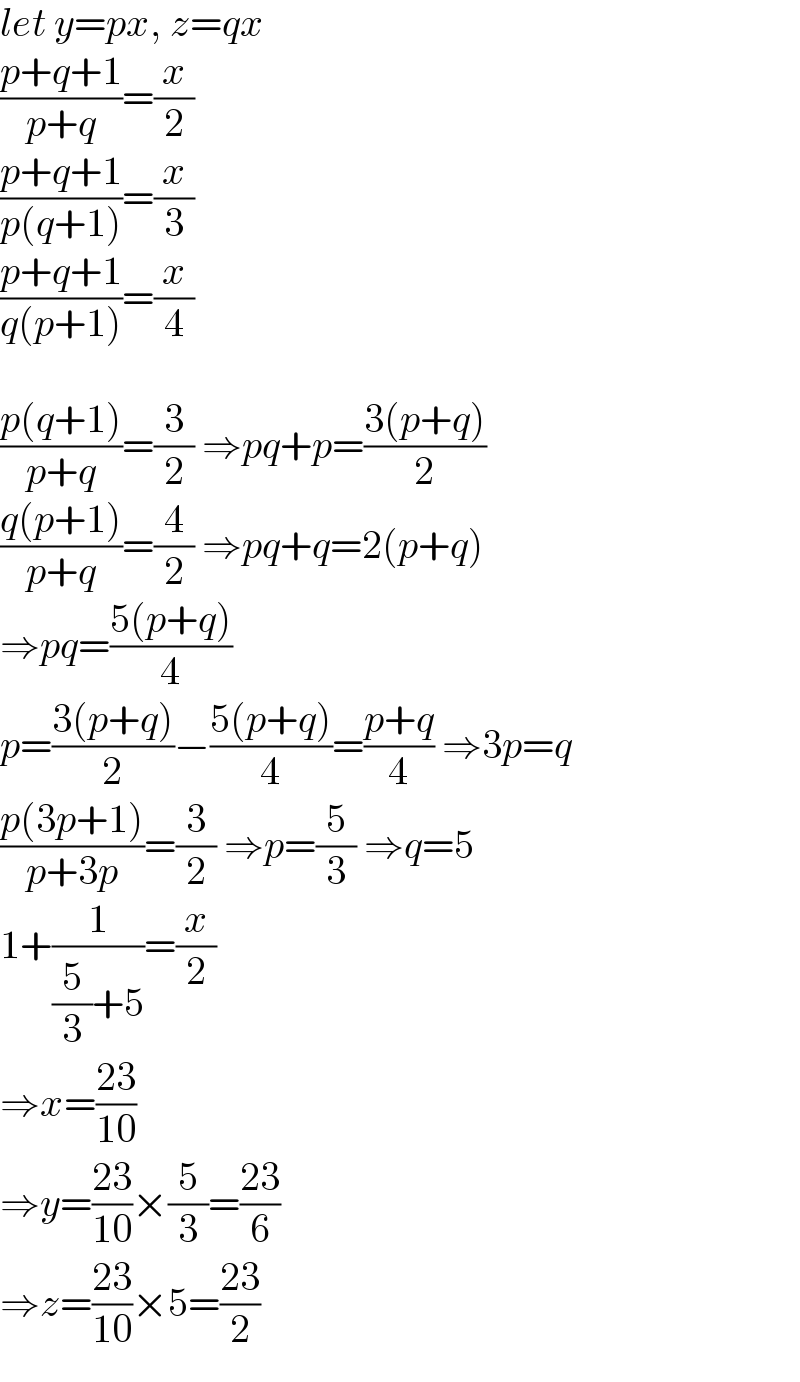
$${let}\:{y}={px},\:{z}={qx} \\ $$$$\frac{{p}+{q}+\mathrm{1}}{{p}+{q}}=\frac{{x}}{\mathrm{2}} \\ $$$$\frac{{p}+{q}+\mathrm{1}}{{p}\left({q}+\mathrm{1}\right)}=\frac{{x}}{\mathrm{3}} \\ $$$$\frac{{p}+{q}+\mathrm{1}}{{q}\left({p}+\mathrm{1}\right)}=\frac{{x}}{\mathrm{4}} \\ $$$$ \\ $$$$\frac{{p}\left({q}+\mathrm{1}\right)}{{p}+{q}}=\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow{pq}+{p}=\frac{\mathrm{3}\left({p}+{q}\right)}{\mathrm{2}} \\ $$$$\frac{{q}\left({p}+\mathrm{1}\right)}{{p}+{q}}=\frac{\mathrm{4}}{\mathrm{2}}\:\Rightarrow{pq}+{q}=\mathrm{2}\left({p}+{q}\right) \\ $$$$\Rightarrow{pq}=\frac{\mathrm{5}\left({p}+{q}\right)}{\mathrm{4}} \\ $$$${p}=\frac{\mathrm{3}\left({p}+{q}\right)}{\mathrm{2}}−\frac{\mathrm{5}\left({p}+{q}\right)}{\mathrm{4}}=\frac{{p}+{q}}{\mathrm{4}}\:\Rightarrow\mathrm{3}{p}={q} \\ $$$$\frac{{p}\left(\mathrm{3}{p}+\mathrm{1}\right)}{{p}+\mathrm{3}{p}}=\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow{p}=\frac{\mathrm{5}}{\mathrm{3}}\:\Rightarrow{q}=\mathrm{5} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{5}}{\mathrm{3}}+\mathrm{5}}=\frac{{x}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{23}}{\mathrm{10}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{23}}{\mathrm{10}}×\frac{\mathrm{5}}{\mathrm{3}}=\frac{\mathrm{23}}{\mathrm{6}} \\ $$$$\Rightarrow{z}=\frac{\mathrm{23}}{\mathrm{10}}×\mathrm{5}=\frac{\mathrm{23}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 30/Sep/22
![an other way: ((x+y+z)/(xy+zx))=(1/2) ⇒xy+zx=2(x+y+z) ...(i) similarly ⇒yz+xy=3(x+y+z) ...(ii) ⇒zx+yz=4(x+y+z) ...(iii) [(i)+(ii)+(iii)]/2: xy+yz+zx=((9(x+y+z))/2) ...(iv) (iv)−(i): yz=((5(x+y+z))/2)=5λ with λ=((x+y+z)/2) similarly zx=((3(x+y+z))/2)=3λ xy=((x+y+z)/2)=λ (xyz)^2 =15λ^3 ⇒xyz=(√(15λ^3 )) ⇒x=((√(15λ))/5) ⇒y=((√(15λ))/3) ⇒z=((√(15λ))/1) x+y+z=2λ=((1/5)+(1/3)+1)(√(15λ)) ⇒(√(15λ))=((23)/2) ⇒x=((23)/(2×5))=((23)/(10)) ⇒y=((23)/(2×3))=((23)/6) ⇒z=((23)/2)](https://www.tinkutara.com/question/Q177086.png)
$${an}\:{other}\:{way}: \\ $$$$\frac{{x}+{y}+{z}}{{xy}+{zx}}=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\Rightarrow{xy}+{zx}=\mathrm{2}\left({x}+{y}+{z}\right)\:\:\:…\left({i}\right) \\ $$$${similarly} \\ $$$$\Rightarrow{yz}+{xy}=\mathrm{3}\left({x}+{y}+{z}\right)\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow{zx}+{yz}=\mathrm{4}\left({x}+{y}+{z}\right)\:\:\:…\left({iii}\right) \\ $$$$\left[\left({i}\right)+\left({ii}\right)+\left({iii}\right)\right]/\mathrm{2}: \\ $$$${xy}+{yz}+{zx}=\frac{\mathrm{9}\left({x}+{y}+{z}\right)}{\mathrm{2}}\:\:\:…\left({iv}\right) \\ $$$$\left({iv}\right)−\left({i}\right): \\ $$$${yz}=\frac{\mathrm{5}\left({x}+{y}+{z}\right)}{\mathrm{2}}=\mathrm{5}\lambda\:{with}\:\lambda=\frac{{x}+{y}+{z}}{\mathrm{2}} \\ $$$${similarly} \\ $$$${zx}=\frac{\mathrm{3}\left({x}+{y}+{z}\right)}{\mathrm{2}}=\mathrm{3}\lambda \\ $$$${xy}=\frac{{x}+{y}+{z}}{\mathrm{2}}=\lambda \\ $$$$\left({xyz}\right)^{\mathrm{2}} =\mathrm{15}\lambda^{\mathrm{3}} \\ $$$$\Rightarrow{xyz}=\sqrt{\mathrm{15}\lambda^{\mathrm{3}} } \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{15}\lambda}}{\mathrm{5}} \\ $$$$\Rightarrow{y}=\frac{\sqrt{\mathrm{15}\lambda}}{\mathrm{3}} \\ $$$$\Rightarrow{z}=\frac{\sqrt{\mathrm{15}\lambda}}{\mathrm{1}} \\ $$$${x}+{y}+{z}=\mathrm{2}\lambda=\left(\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right)\sqrt{\mathrm{15}\lambda} \\ $$$$\Rightarrow\sqrt{\mathrm{15}\lambda}=\frac{\mathrm{23}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{23}}{\mathrm{2}×\mathrm{5}}=\frac{\mathrm{23}}{\mathrm{10}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{23}}{\mathrm{2}×\mathrm{3}}=\frac{\mathrm{23}}{\mathrm{6}} \\ $$$$\Rightarrow{z}=\frac{\mathrm{23}}{\mathrm{2}} \\ $$
