Question Number 177040 by cortano1 last updated on 30/Sep/22

Answered by mr W last updated on 30/Sep/22

$${total}\:{number}\:{of}\:\mathrm{9}−{digit}\:{numbers}\:{is}: \\ $$$$\mathrm{9}!=\mathrm{362880} \\ $$$$ \\ $$$${number}\:{of}\:{those}\:{which}\:{are}\:{divisible} \\ $$$${by}\:\mathrm{4}\:{is}: \\ $$$${last}\:{digit}\:{is}\:\mathrm{2}:\: \\ $$$$\mathrm{xxxxxxx12}/\mathrm{32}/\mathrm{52}/\mathrm{72}/\mathrm{92}\:\Rightarrow\:\mathrm{5}×\mathrm{7}! \\ $$$${last}\:{digit}\:{is}\:\mathrm{4}:\: \\ $$$$\mathrm{xxxxxxx24}/\mathrm{64}/\mathrm{84}\:\Rightarrow\mathrm{3}×\mathrm{7}! \\ $$$${last}\:{digit}\:{is}\:\mathrm{6}:\: \\ $$$$\mathrm{xxxxxxx16}/\mathrm{36}/\mathrm{56}/\mathrm{76}/\mathrm{96}\:\Rightarrow\mathrm{5}×\mathrm{7}! \\ $$$${last}\:{digit}\:{is}\:\mathrm{8}:\: \\ $$$$\mathrm{xxxxxxx28}/\mathrm{48}/\mathrm{68}\:\Rightarrow\mathrm{3}×\mathrm{7}! \\ $$$$\Sigma:\:\mathrm{16}×\mathrm{7}!=\mathrm{80640} \\ $$
Commented by cortano1 last updated on 30/Sep/22
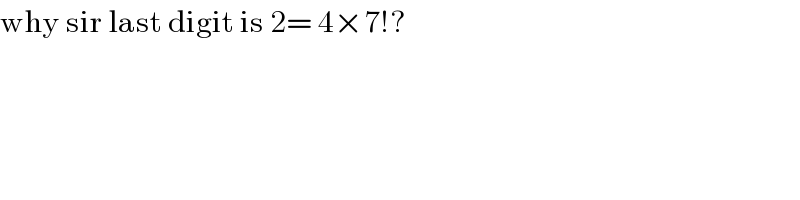
$$\mathrm{why}\:\mathrm{sir}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{is}\:\mathrm{2}=\:\mathrm{4}×\mathrm{7}!? \\ $$
Commented by mr W last updated on 30/Sep/22
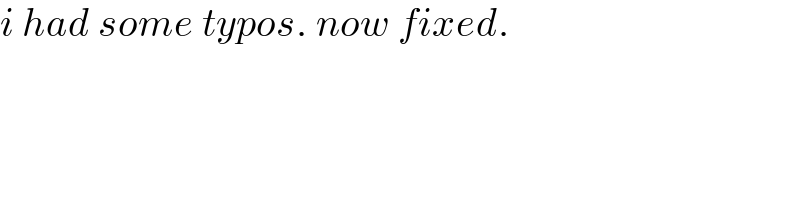
$${i}\:{had}\:{some}\:{typos}.\:{now}\:{fixed}. \\ $$
Commented by Tawa11 last updated on 03/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
