Question Number 177044 by Ar Brandon last updated on 30/Sep/22
Answered by a.lgnaoui last updated on 30/Sep/22

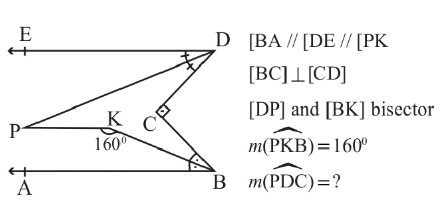
$$\Sigma\:{angles}\:{interieures}=\Sigma{angles}\:{exterieures} \\ $$$$\frac{\measuredangle{B}}{\mathrm{2}}+\measuredangle{KPD}+\frac{\measuredangle{D}}{\mathrm{2}}=\mathrm{90} \\ $$$$\measuredangle{EDD}=\frac{\measuredangle{D}}{\mathrm{2}}\:\:\:\left({PK}\mid\mid\:{ED}\right) \\ $$$$\:\frac{\measuredangle{B}}{\mathrm{2}}+\measuredangle{D}=\mathrm{90} \\ $$$$\:{quadrilateral}\:\:{APKB}=\mathrm{360}^{°} \\ $$$$\:\frac{{B}}{\mathrm{2}}=\mathrm{360}−\mathrm{180}−\mathrm{160}=\mathrm{20}^{°} \\ $$$${donc}\:\:\measuredangle{D}=\mathrm{90}−\mathrm{20}=\mathrm{70} \\ $$$$ \\ $$$${m}\left({PDC}\right)=\frac{\measuredangle{D}}{\mathrm{2}}=\mathrm{35}^{°} \\ $$
Commented by Ar Brandon last updated on 30/Sep/22
Merci monsieur
