Question Number 177046 by Ar Brandon last updated on 30/Sep/22

Answered by som(math1967) last updated on 30/Sep/22

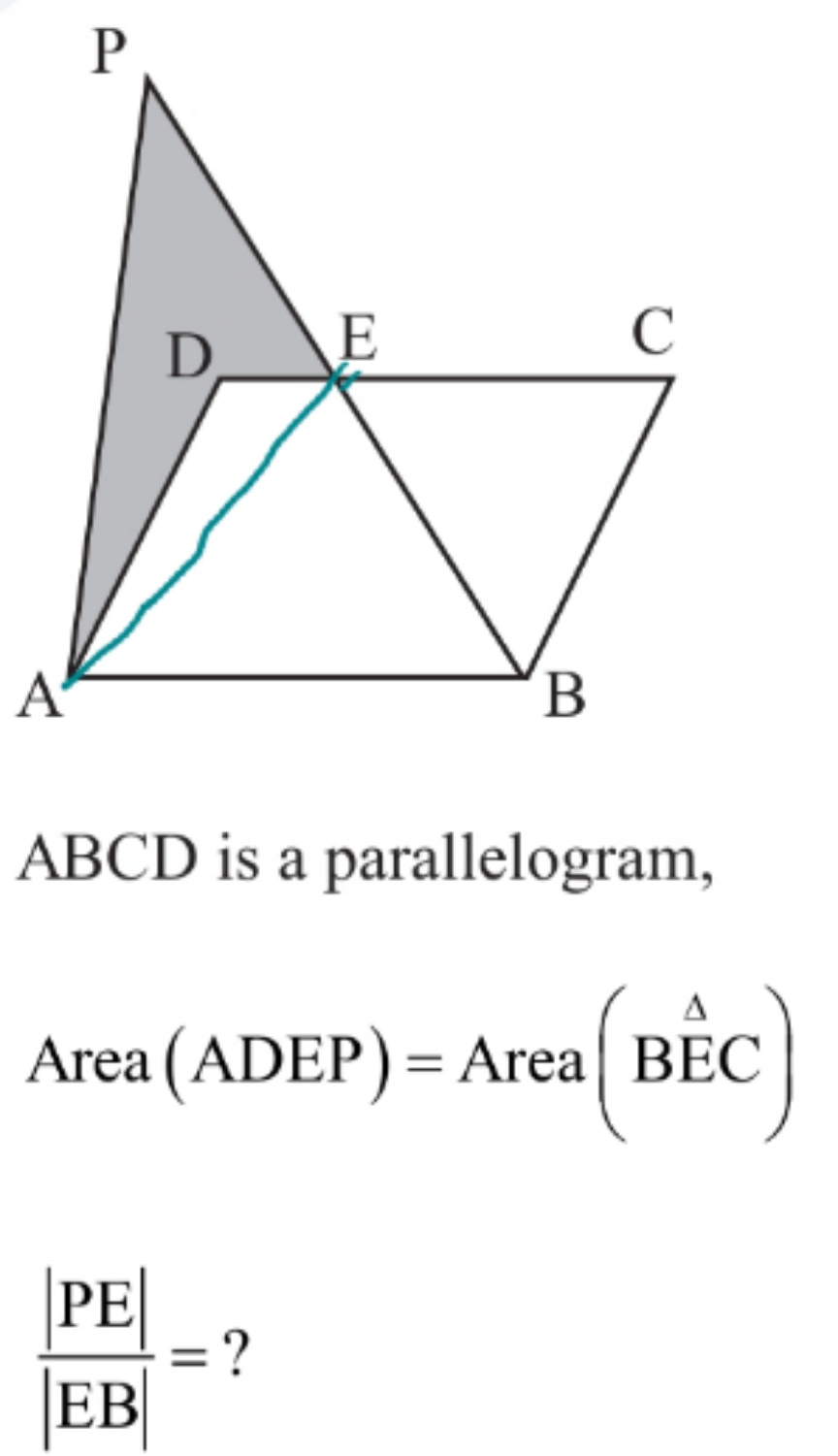
$${Area}\left(\bigtriangleup{ADE}+\bigtriangleup{BEC}\right)=\frac{\mathrm{1}}{\mathrm{2}}{AreaABCD} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{x}}{\mathrm{2}}\:\left({let}\right) \\ $$$${Area}\bigtriangleup{AEB}=\frac{\mathrm{1}}{\mathrm{2}}{ABCD}=\frac{{x}}{\mathrm{2}} \\ $$$${Area}\left({ADEP}+\bigtriangleup{ADE}\right) \\ $$$$=\bigtriangleup{BEC}+\bigtriangleup{ADE}=\frac{{x}}{\mathrm{2}} \\ $$$$\:{area}\bigtriangleup{APE}={Area}\left({ADEP}+\bigtriangleup{ADE}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{{x}}{\mathrm{2}} \\ $$$$\therefore{ar}\bigtriangleup{APE}={ar}\bigtriangleup{AEB} \\ $$$$\Rightarrow\frac{{ar}\bigtriangleup{APE}}{{ar}\bigtriangleup{AEB}}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$\Rightarrow\frac{{PE}}{{EB}}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$ \\ $$
Commented by som(math1967) last updated on 30/Sep/22
Commented by Ar Brandon last updated on 30/Sep/22
Thank you Sir
