Question Number 177047 by Ar Brandon last updated on 30/Sep/22
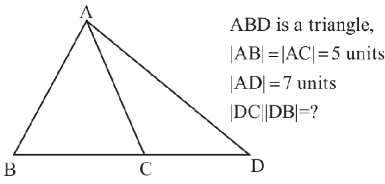
Answered by som(math1967) last updated on 30/Sep/22
![cosD=((7^2 +DC^2 −5^2 )/(2×7DC))=((24+DC^2 )/(14DC)) again cosD=((7^2 +DB^2 −5^2 )/(2×7×DB))=((24+DB^2 )/(14DB)) ((24+DC^2 )/(14DC))=((24+DB^2 )/(14DB)) ⇒24DB+DB×DC^2 =24DC+DC×DB^2 ⇒24(DB−DC)=DB×DC(DB−DC) DB×DC=24 [∵DB≠DC]](https://www.tinkutara.com/question/Q177069.png)
$${cosD}=\frac{\mathrm{7}^{\mathrm{2}} +{DC}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}{DC}}=\frac{\mathrm{24}+{DC}^{\mathrm{2}} }{\mathrm{14}{DC}} \\ $$$${again}\:\:{cosD}=\frac{\mathrm{7}^{\mathrm{2}} +{DB}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×{DB}}=\frac{\mathrm{24}+{DB}^{\mathrm{2}} }{\mathrm{14}{DB}} \\ $$$$\frac{\mathrm{24}+{DC}^{\mathrm{2}} }{\mathrm{14}{DC}}=\frac{\mathrm{24}+{DB}^{\mathrm{2}} }{\mathrm{14}{DB}} \\ $$$$\Rightarrow\mathrm{24}{DB}+{DB}×{DC}^{\mathrm{2}} =\mathrm{24}{DC}+{DC}×{DB}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{24}\left({DB}−{DC}\right)={DB}×{DC}\left({DB}−{DC}\right) \\ $$$${DB}×{DC}=\mathrm{24}\:\left[\because{DB}\neq{DC}\right] \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 30/Sep/22
Thank you Sir
Answered by HeferH last updated on 30/Sep/22

$$\: \\ $$$$\:{Let}\:{h}\:{be}\:{the}\:{height}\:{of}\:\bigtriangleup{ABC}\: \\ $$$$\:{h}^{\mathrm{2}} \:=\:\mathrm{25}\:−\:\frac{{BC}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:{h}^{\mathrm{2}} \:+\:\left(\frac{{BC}}{\mathrm{2}}\:+\:{CD}\right)^{\mathrm{2}} \:=\:\mathrm{49} \\ $$$$\:{CD}^{\mathrm{2}} \:+\:\left({CD}\right)\left({BC}\right)=\mathrm{24} \\ $$$$\:{CD}\left({CD}\:+\:{BC}\right)\:=\:\mathrm{24} \\ $$$$\:{CD}\left({DB}\right)=\mathrm{24} \\ $$
Commented by Ar Brandon last updated on 30/Sep/22
Thank you Sir
