Question-177071

Question Number 177071 by cortano1 last updated on 30/Sep/22

Commented by Frix last updated on 30/Sep/22

$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$

Commented by Frix last updated on 30/Sep/22

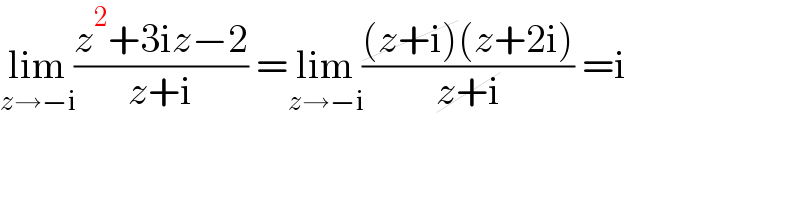
lim_(z→−i) ((z^2 +3iz−2)/(z+i)) =lim_(z→−i) (((z+i)(z+2i))/(z+i)) =i

$$\underset{{z}\rightarrow−\mathrm{i}} {\mathrm{lim}}\frac{{z}^{\mathrm{2}} +\mathrm{3i}{z}−\mathrm{2}}{{z}+\mathrm{i}}\:=\underset{{z}\rightarrow−\mathrm{i}} {\mathrm{lim}}\frac{\cancel{\left({z}+\mathrm{i}\right)}\left({z}+\mathrm{2i}\right)}{\cancel{{z}+\mathrm{i}}}\:=\mathrm{i} \\ $$

Answered by Frix last updated on 30/Sep/22

z=re^(iθ) −i ((z^3 +3iz−2)/(z+i))= =(r^2 cos 2θ +3rsin θ −3+((cos θ +sin θ)/r))+ +(r^2 sin 2θ −3rcos θ +3+((cos θ −sin θ)/r))i z→−i ⇔ r→0 and the red terms are undefined ⇒ limit doesn′t exist

$${z}={r}\mathrm{e}^{\mathrm{i}\theta} −\mathrm{i} \\ $$$$\frac{{z}^{\mathrm{3}} +\mathrm{3i}{z}−\mathrm{2}}{{z}+\mathrm{i}}= \\ $$$$=\left({r}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\theta\:+\mathrm{3}{r}\mathrm{sin}\:\theta\:−\mathrm{3}+\frac{\mathrm{cos}\:\theta\:+\mathrm{sin}\:\theta}{{r}}\right)+ \\ $$$$\:\:\:\:\:+\left({r}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta\:−\mathrm{3}{r}\mathrm{cos}\:\theta\:+\mathrm{3}+\frac{\mathrm{cos}\:\theta\:−\mathrm{sin}\:\theta}{{r}}\right)\mathrm{i} \\ $$$${z}\rightarrow−\mathrm{i}\:\Leftrightarrow\:{r}\rightarrow\mathrm{0}\:\mathrm{and}\:\mathrm{the}\:\mathrm{red}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{undefined} \\ $$$$\Rightarrow\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$

Facebook Tweet Pin

Question-177071

Leave a Reply Cancel reply