Question Number 177214 by mr W last updated on 02/Oct/22

Commented by mr W last updated on 02/Oct/22

$${the}\:{friction}\:{coefficient}\:{between}\:{the} \\ $$$${thin}\:{rod}\:{and}\:{the}\:{ground}\:{as}\:{well}\:{as}\:{the} \\ $$$${wall}\:{is}\:\mu.\:{the}\:{length}\:{of}\:{the}\:{rod}\:{is}\:{L}.\: \\ $$$${find}\:{the}\:{condition}\:{which}\:{a}\:{and}\:{b} \\ $$$${must}\:{fulfill}\:{such}\:{that}\:{the}\:{rod}\:{can} \\ $$$${rest}\:{in}\:{equilibrium}\:{and}\:{is}\:{about}\:{to} \\ $$$${slip}\:{as}\:{shown}. \\ $$
Commented by mahdipoor last updated on 02/Oct/22
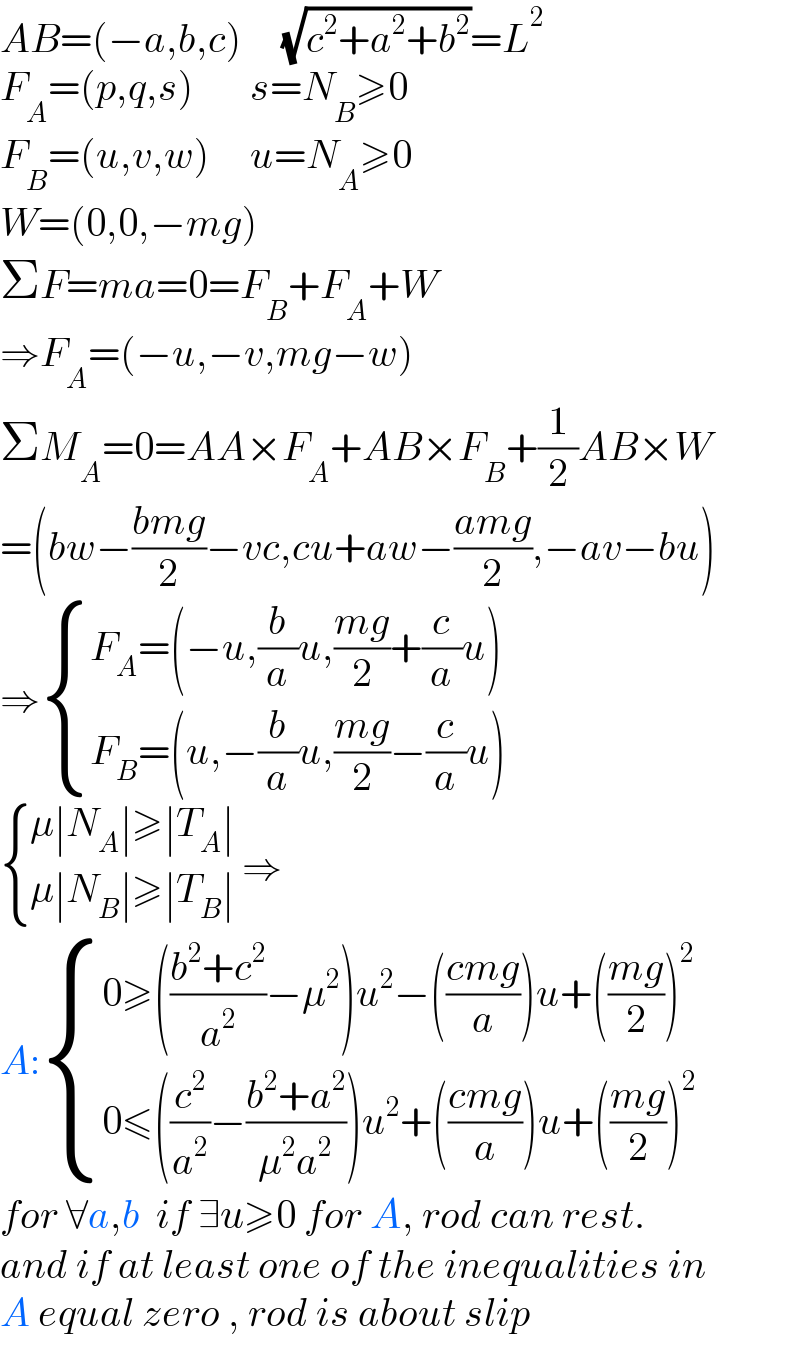
$${AB}=\left(−{a},{b},{c}\right)\:\:\:\:\:\sqrt{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }={L}^{\mathrm{2}} \\ $$$${F}_{{A}} =\left({p},{q},{s}\right)\:\:\:\:\:\:\:{s}={N}_{{B}} \geqslant\mathrm{0} \\ $$$${F}_{{B}} =\left({u},{v},{w}\right)\:\:\:\:\:{u}={N}_{{A}} \geqslant\mathrm{0} \\ $$$${W}=\left(\mathrm{0},\mathrm{0},−{mg}\right) \\ $$$$\Sigma{F}={ma}=\mathrm{0}={F}_{{B}} +{F}_{{A}} +{W} \\ $$$$\Rightarrow{F}_{{A}} =\left(−{u},−{v},{mg}−{w}\right) \\ $$$$\Sigma{M}_{{A}} =\mathrm{0}={AA}×{F}_{{A}} +{AB}×{F}_{{B}} +\frac{\mathrm{1}}{\mathrm{2}}{AB}×{W} \\ $$$$=\left({bw}−\frac{{bmg}}{\mathrm{2}}−{vc},{cu}+{aw}−\frac{{amg}}{\mathrm{2}},−{av}−{bu}\right) \\ $$$$\Rightarrow\begin{cases}{{F}_{{A}} =\left(−{u},\frac{{b}}{{a}}{u},\frac{{mg}}{\mathrm{2}}+\frac{{c}}{{a}}{u}\right)}\\{{F}_{{B}} =\left({u},−\frac{{b}}{{a}}{u},\frac{{mg}}{\mathrm{2}}−\frac{{c}}{{a}}{u}\right)}\end{cases} \\ $$$$\begin{cases}{\mu\mid{N}_{{A}} \mid\geqslant\mid{T}_{{A}} \mid}\\{\mu\mid{N}_{{B}} \mid\geqslant\mid{T}_{{B}} \mid}\end{cases}\:\Rightarrow \\ $$$${A}:\begin{cases}{\mathrm{0}\geqslant\left(\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mu^{\mathrm{2}} \right){u}^{\mathrm{2}} −\left(\frac{{cmg}}{{a}}\right){u}+\left(\frac{{mg}}{\mathrm{2}}\right)^{\mathrm{2}} }\\{\mathrm{0}\leqslant\left(\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} }{\mu^{\mathrm{2}} {a}^{\mathrm{2}} }\right){u}^{\mathrm{2}} +\left(\frac{{cmg}}{{a}}\right){u}+\left(\frac{{mg}}{\mathrm{2}}\right)^{\mathrm{2}} }\end{cases} \\ $$$${for}\:\forall{a},{b}\:\:{if}\:\exists{u}\geqslant\mathrm{0}\:{for}\:{A},\:{rod}\:{can}\:{rest}. \\ $$$${and}\:{if}\:{at}\:{least}\:{one}\:{of}\:{the}\:{inequalities}\:{in} \\ $$$${A}\:{equal}\:{zero}\:,\:{rod}\:{is}\:{about}\:{slip} \\ $$
Commented by mr W last updated on 02/Oct/22

$${thanks}\:{for}\:{your}\:{solution}\:{sir}! \\ $$$${i}\:{need}\:{some}\:{time}\:{to}\:{follow}\:{it}. \\ $$
Answered by mr W last updated on 03/Oct/22

Commented by mr W last updated on 03/Oct/22

$$\boldsymbol{{background}}\:\boldsymbol{{knowledge}}\:\mathrm{1} \\ $$$${an}\:{object}\:{doesn}'{t}\:{slip},\:{when}\:{the}\:{angle} \\ $$$$\theta\:{between}\:{the}\:{resultant}\:{contact}\:{force} \\ $$$${and}\:{the}\:{normal}\:{of}\:{the}\:{contact}\:{surface} \\ $$$${is}\:{less}\:{than}\:\theta^{\ast} \:{which}\:{is}\:\mathrm{tan}^{−\mathrm{1}} \mu.\: \\ $$$${the}\:{object}\:{is}\:{about}\:{to}\:{slip},\: \\ $$$${when}\:\theta=\theta^{\ast} =\mathrm{tan}^{−\mathrm{1}} \mu. \\ $$
Commented by mr W last updated on 02/Oct/22
Commented by mr W last updated on 03/Oct/22

$${let}\:\xi=\frac{{a}}{{L}},\:\eta=\frac{{b}}{{L}} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }={L}\sqrt{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} } \\ $$$${h}=\sqrt{{L}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }={L}\sqrt{\mathrm{1}−\xi^{\mathrm{2}} −\eta^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:\phi=\frac{{a}}{{c}}=\frac{\xi}{\:\sqrt{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }} \\ $$$$ \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} \leqslant\mu \\ $$$$\mathrm{tan}\:\theta_{\mathrm{2}} \leqslant\mu\: \\ $$$$\Rightarrow\mathrm{cos}\:\theta_{\mathrm{2}} \geqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }} \\ $$$$ \\ $$$$\mathrm{tan}\:\beta=\frac{{c}}{{h}}=\frac{\sqrt{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−\xi^{\mathrm{2}} −\eta^{\mathrm{2}} }} \\ $$$$\mathrm{sin}\:\varphi×\mathrm{sin}\:\phi=\mathrm{cos}\:\theta_{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\frac{\mathrm{cos}\:\theta_{\mathrm{2}} }{\mathrm{sin}\:\phi}\geqslant\frac{\mathrm{1}}{\xi}\sqrt{\frac{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{tan}\:\varphi\geqslant\sqrt{\frac{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }{\mu^{\mathrm{2}} \xi^{\mathrm{2}} −\eta^{\mathrm{2}} }} \\ $$$$ \\ $$$$\frac{{CD}}{{CB}}=\frac{\mathrm{sin}\:\left(\beta+\varphi\right)}{\mathrm{sin}\:\varphi}=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\varphi}+\mathrm{cos}\:\beta \\ $$$$\frac{{CD}}{{AC}}=\frac{\mathrm{sin}\:\left(\beta−\theta_{\mathrm{1}} \right)}{\mathrm{sin}\:\theta_{\mathrm{1}} }=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\theta_{\mathrm{1}} }−\mathrm{cos}\:\beta \\ $$$$\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\theta_{\mathrm{1}} }−\mathrm{cos}\:\beta=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\varphi}+\mathrm{cos}\:\beta \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\theta_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=\frac{\mathrm{2}}{\mathrm{tan}\:\beta} \\ $$$$\frac{\mathrm{1}}{\mu}−\frac{\sqrt{\mu^{\mathrm{2}} \xi^{\mathrm{2}} −\eta^{\mathrm{2}} }}{\:\sqrt{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }}\leqslant\frac{\mathrm{2}\sqrt{\mathrm{1}−\xi^{\mathrm{2}} −\eta^{\mathrm{2}} }}{\:\sqrt{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }} \\ $$$$\begin{array}{|c|}{\mathrm{2}\sqrt{\mathrm{1}−\xi^{\mathrm{2}} −\eta^{\mathrm{2}} }+\sqrt{\mu^{\mathrm{2}} \xi^{\mathrm{2}} −\eta^{\mathrm{2}} }−\frac{\sqrt{\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }}{\mu}\geqslant\mathrm{0}}\\\hline\end{array} \\ $$
Commented by mr W last updated on 03/Oct/22

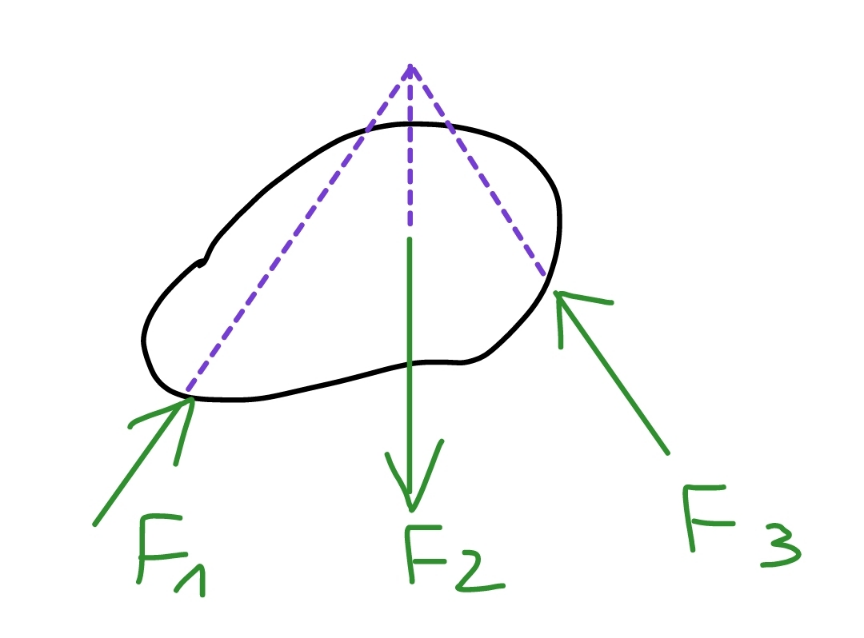
$$\boldsymbol{{background}}\:\boldsymbol{{knowledge}}\:\mathrm{2} \\ $$$${when}\:{an}\:{object}\:{is}\:{in}\:{equilibrium}\:{under} \\ $$$${the}\:{action}\:{of}\:{three}\:{forces},\:{then}\:{these} \\ $$$${three}\:{forces}\:{must}\:{intersect}\:{at}\:{the} \\ $$$${same}\:{point}\:{and}\:{their}\:{sum}\:\left({vector}\right)\:{is} \\ $$$${zero}. \\ $$
Commented by mr W last updated on 03/Oct/22

Commented by mr W last updated on 02/Oct/22

Commented by mr W last updated on 02/Oct/22

Commented by mr W last updated on 02/Oct/22

$$=\:{END}\:= \\ $$
Commented by mr W last updated on 03/Oct/22

$${following}\:{diagram}\:{shows}\:{the}\:{range} \\ $$$${for}\:{a}\:{and}\:{b}\:{such}\:{that}\:{the}\:{rod}\:{is}\:{in} \\ $$$${equilibrium}. \\ $$$${example}\:\mu=\mathrm{0}.\mathrm{5}. \\ $$
Commented by mr W last updated on 02/Oct/22

Commented by mahdipoor last updated on 02/Oct/22

$${very}\:{nice}\:{method}\:{for}\:{answer}! \\ $$$${but}\:,\: \\ $$$${in}\:{lemma}\:\mathrm{1}\:{only}\:{correctness}\:{of}\:\mu{N}\leqslant{T} \\ $$$${and} \\ $$$${in}\:{lemma}\:\mathrm{2}\:{only}\:\Sigma\:{Moment}\:{is}\:{zero} \\ $$$${are}\:{guaranteed}\:. \\ $$$${how}\:{about}\:\Sigma{F}=\mathrm{0}\:? \\ $$$${if}\:\Sigma{F}=\mathrm{0}\:{then}\:{lemma}\:\mathrm{2}\:{is}\:{true}. \\ $$$${i}\:{think}\:{balance}\:{of}\:{forces}\:{is}\:{not}\:{in}\:{solution} \\ $$$${and}\:{that}'{s}\:{why}\:\left({mg}\right)\:{is}\:{ineffective} \\ $$$${in}\:{equilibrium}\:{conditions}. \\ $$
Commented by mr W last updated on 03/Oct/22

$$\left.\mathrm{1}\right)\:\mu{N}\leqslant{T}\:{means}\:\theta\leqslant\mathrm{tan}^{−\mathrm{1}} \mu \\ $$$$\left.\mathrm{2}\right)\:{here}\:{i}\:{just}\:{want}\:{to}\:{say}:\: \\ $$$$\:\:\:\:\:\:{if}\:{equilibrium},\:{then}\:\mathrm{3}\:{forces} \\ $$$$\:\:\:\:\:\:{intersect}\:{at}\:{same}\:{point}. \\ $$$$\:\:\:\:\:\:{it}\:{is}\:{not}\:{said}:\:{if}\:\mathrm{3}\:{forces}\:{intersect} \\ $$$$\:\:\:\:\:\:{at}\:{same}\:{point},\:{then}\:{equilbrium}. \\ $$$$\:\:\:\:\:\:{certainly}\:{i}\:{know}\:\underset{\mathrm{1},\mathrm{2},\mathrm{3}} {\sum}{F}_{{i}} \:{should}\:{be} \\ $$$$\:\:\:\:\:\:{zero}\:{for}\:{equilibrium}.\:{but}\:{for}\:{solving} \\ $$$$\:\:\:\:\:\:{this}\:{problem},\:{i}\:{only}\:{need}\:{to}\:{know} \\ $$$$\:\:\:\:\:\:“{if}\:{equilibrium},\:{then}\:\mathrm{3}\:{forces} \\ $$$$\:\:\:\:\:\:{intersect}\:{at}\:{same}\:{point}''.\:{that} \\ $$$$\:\:\:\:\:\:\Sigma{F}=\mathrm{0}\:{is}\:{also}\:{true},\:{is}\:{clear}.\:{but}\:{i} \\ $$$$\:\:\:\:\:\:{don}'{t}\:{need}\:{this}\:{for}\:{solving}\:{the} \\ $$$$\:\:\:\:\:\:{problem}. \\ $$$$\left.\mathrm{3}\right)\:\:{for}\:{solving}\:{the}\:{problem},\:{only} \\ $$$$\:\:\:\:\:\:{the}\:{directions}\:{of}\:{the}\:{forces}\:{are} \\ $$$$\:\:\:\:\:\:{interesting},\:{not}\:{their}\:{sizes}.\: \\ $$$$\:\:\:\:\:\:{therefore}\:{the}\:{weight}\:{of}\:{the}\:{rod}\:{mg} \\ $$$$\:\:\:\:\:\:{doesn}'{t}\:{affect}\:{the}\:{result}.\:{in}\:{fact} \\ $$$$\:\:\:\:\:\:{it}\:{is}\:{more}\:{a}\:{question}\:{of}\:{geometry}. \\ $$
Commented by mahdipoor last updated on 02/Oct/22

$${thank}\:{you}\:,\:{you}\:{are}\:{right}\:!\:\heartsuit \\ $$
Commented by mahdipoor last updated on 03/Oct/22

$${and}\:{one}\:{more}\:{question}: \\ $$$${in}\:{special}\:{case}:\:{let}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={L}^{\mathrm{2}} \:\left(\Rightarrow\:{h}=\mathrm{0}\right. \\ $$$$\left.\:{and}\:\xi^{\mathrm{2}} +\eta^{\mathrm{2}} =\mathrm{1}\right)\:\:\: \\ $$$${its}\:{means}\:,\:{rod}\:{is}\:{horizontal} \\ $$$${its}\:{seems}\:{that}\:{in}\:{this}\:{case},\mathrm{0}\leqslant\xi\leqslant\mathrm{1} \\ $$$${and}\:\mu\:{is}\:{ineffective} \\ $$$${from}\:{your}\:{answer}\:: \\ $$$$\mathrm{0}+\sqrt{\mu^{\mathrm{2}} \xi^{\mathrm{2}} −\eta^{\mathrm{2}} }−\frac{\mathrm{1}}{\mu}\geqslant\mathrm{0}\:\Rightarrow\:\xi\geqslant\frac{\mathrm{1}}{\mu}\:\: \\ $$$${what}\:{is}\:{wrong}? \\ $$
Commented by Tawa11 last updated on 03/Oct/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Commented by mr W last updated on 03/Oct/22

$$\boldsymbol{{to}}\:\boldsymbol{{mahdipoor}}\:\boldsymbol{{sir}}: \\ $$$${thanks}\:{for}\:{your}\:{feedback}!\: \\ $$$${i}\:{appreciate}\:{such}\:{substantial}\:{feedback} \\ $$$${very}\:{much}. \\ $$$${your}\:{question}\:{is}\:{interesting}.\:{i}\:{also} \\ $$$${noticed}\:{this}\:{issue}\:{as}\:{i}\:{saw}\:{the}\:{graph} \\ $$$${for}\:{the}\:{case}\:\mu=\mathrm{2},\:{which}\:{i}\:{didn}'{t}\:{post}. \\ $$$${i}\:{considered}\:{to}\:{study}\:{it}\:{and}\:{try}\:{to}\: \\ $$$${explain}\:{it}\:{later},\:{when}\:{i}\:{have}\:{more}\:{time}. \\ $$$${since}\:{you}\:{have}\:{asked}\:{the}\:{same}\: \\ $$$${question}\:{about}\:{this}\:{issue},\:{i}\:{have}\:{spent}\: \\ $$$${some}\:{time}\:{to}\:{take}\:{a}\:{closer}\:{look}\:{at}\:{it}. \\ $$$${i}\:{think}\:{it}\:{is}\:{not}\:{a}\:{fault}\:{in}\:{the} \\ $$$${solution}.\:{it}\:{can}\:{be}\:{explained}\:{as} \\ $$$${following}. \\ $$
Commented by mr W last updated on 03/Oct/22

Commented by mr W last updated on 03/Oct/22

$${in}\:{case}\:{of}\:\mu\geqslant\mathrm{1},\:\theta^{\ast} =\mathrm{tan}^{−\mathrm{1}} \mu\geqslant\mathrm{45}°. \\ $$$${in}\:{this}\:{case}\:{the}\:{rod}\:{can}\:{lie}\:{in}\:{a}\:{very} \\ $$$${flat}\:{position},\:{close}\:{to}\:{horizontal}\:{or} \\ $$$${even}\:{in}\:{horizontal}\:{position},\:{and}\:{still} \\ $$$${be}\:{kept}\:{in}\:{equilbrium}.\:{we}\:{can}\:{see}\:{in} \\ $$$${the}\:{diagram}\:{above}\:{that}\:{within}\:{the} \\ $$$${angles}\:\theta^{\ast} \:{contact}\:{forces}\:{R}_{\mathrm{1}} \:{and}\:{R}_{\mathrm{2}} \: \\ $$$${can}\:{be}\:{found}\:{which}\:{meet}\:{the}\:{mg}\:{at} \\ $$$${the}\:{same}\:{point},\:{therefore}\:{a}\:{equilibrium} \\ $$$${state}\:{is}\:{possible}.\:{certainly}\:{a}\:{absolutely} \\ $$$${horizontal}\:{equilibrium}\:{position}\:{is} \\ $$$${just}\:{theory}.\:{but}\:{mathematically}\:{it}\:{is}\: \\ $$$${possible}. \\ $$
Commented by mr W last updated on 03/Oct/22

Commented by mr W last updated on 03/Oct/22

Commented by mr W last updated on 03/Oct/22

$${for}\:\mu<\mathrm{1},\:\theta^{\ast} <\mathrm{45}°,\:{we}\:{can}\:{see}\:{that}\:{an} \\ $$$${equilibrium}\:{state}\:{in}\:{such}\:{a}\:{flat}\: \\ $$$${position}\:{is}\:{not}\:{possible},\:{because}\:{we} \\ $$$${can}\:{not}\:{find}\:{within}\:{the}\:{angles}\:\theta^{\ast} \:{such} \\ $$$${contact}\:{forces}\:{R}_{\mathrm{1}} \:{and}\:{R}_{\mathrm{2}} \:{which}\:{meet} \\ $$$${the}\:{mg}\:{at}\:{the}\:{same}\:{point}.\:{in}\:{this}\:{case} \\ $$$${c}<{L},\:{i}.{e}.\:\xi^{\mathrm{2}} +\eta^{\mathrm{2}} <\mathrm{1}. \\ $$
Commented by mr W last updated on 03/Oct/22

Commented by mahdipoor last updated on 04/Oct/22

$${exactly}\: \\ $$$${in}\:{this}\:{answer},{it}\:{is}\:{important}\:{that}\:{the} \\ $$$${three}\:{forces}\:{are}\:{concurrent} \\ $$$${in}\:{horizontal}\:{positon},{the}\:{forces}\:{are}\:{parallel} \\ $$$${and}\:{are}\:{not}\:{concurrent}\:. \\ $$$${that}\:{is}\:{why}\:{the}\:{answer}\:{for}\:{this}\:{case}\:{is}\:{fals} \\ $$
