Question Number 177320 by mnjuly1970 last updated on 03/Oct/22
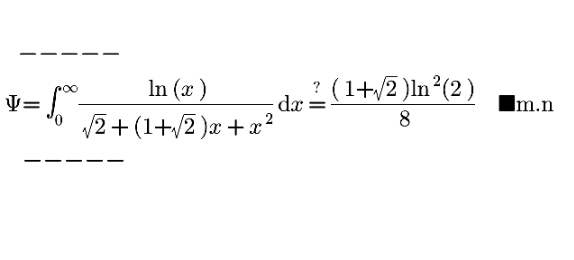
Answered by a.lgnaoui last updated on 04/Oct/22
![(√2) +(1+(√2) )x+x^2 =(x+((1+(√2))/2))^2 −(((√3)/2))^2 =(x+((1+(√2))/2)+((√3)/2))(x+((1+(√2))/2)−((√3)/2)) (1/((x+((1+(√2))/2)−((√3)/2))(x+((1+(√2))/2)+((√3)/2))))=−((2(√3))/3)[(1/((x+((1+(√2) −(√3))/2))))+(1/((x+((1+(√2) +(√3))/2))))] ∫_0 ^∞ ((lnx)/(x^2 +(1+(√2) )x))dx=−((2(√3))/3)∫((1/(x+((1+(√2) −(√3))/2)))+(1/(x+((1+(√3) +(√3))/2))))lnxdx =ln[x(x+((1+(√2) −(√3) )/2))(x+((1+(√2) +(√3) )/2))]_0 ^∞ +((2(√3))/3)∫_0 ^∞ (1/x)((1/(x+((1+(√2) −(√3))/2))))+((1/(x+((1+(√2) +(√3) )/2))))dx (1/(x(x+((1+(√2) −(√3))/2))))=(1/((x+((1+(√2) −(√3))/4))^2 −(((3−((√2) −(√3) −(√6) )/8)))) de meme pour (1/(x(x+((1+(√2^ ) +(√3))/2)))) ona alirs forme (1/(x^2 −a^2 ))=(1/(a^2 [((x/a))^2 −1])) =(2/( (√((√6) +(√3) −(√2) +3))))[Arctan (x+((1+(√2) +(√3))/4))]_0 ^∞ =(π/2)−((8/( (√3) +(√6) +(√2) +3)))arctan (((17+(√2^ ) +(√3) )/4)) ...................](https://www.tinkutara.com/question/Q177340.png)
$$\sqrt{\mathrm{2}}\:+\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right){x}+{x}^{\mathrm{2}} =\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}=−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}+\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}\right] \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}{x}}{{x}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right){x}}{dx}=−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int\left(\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}}{\mathrm{2}}}+\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)\mathrm{ln}{xdx} \\ $$$$=\mathrm{ln}\left[{x}\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}}\left(\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+\left(\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:}{\mathrm{2}}}\right){dx} \\ $$$$\frac{\mathrm{1}}{{x}\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}−\left(\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{6}}\:\right.}{\mathrm{8}}\right)}\:\:{de}\:{meme}\:{pour}\:\frac{\mathrm{1}}{{x}\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}^{\:} }\:+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \\ $$$${ona}\:{alirs}\:{forme}\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \left[\left(\frac{\mathrm{x}}{\mathrm{a}}\right)^{\mathrm{2}} −\mathrm{1}\right]} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\sqrt{\mathrm{6}}\:+\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}\:+\mathrm{3}}}\left[{Arc}\mathrm{tan}\:\left({x}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\pi}{\mathrm{2}}−\left(\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{6}}\:+\sqrt{\mathrm{2}}\:+\mathrm{3}}\right){arc}\mathrm{tan}\:\left(\frac{\mathrm{17}+\sqrt{\mathrm{2}^{\:} }\:+\sqrt{\mathrm{3}}\:}{\mathrm{4}}\right) \\ $$$$………………. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
