Question-177332

Question Number 177332 by mr W last updated on 03/Oct/22

Commented by mr W last updated on 04/Oct/22

the question is to find the maximum value of x such that the rod doesn′t slip. [Q90331]

$${the}\:{question}\:{is}\:{to}\:{find}\:{the}\:{maximum} \\ $$$${value}\:{of}\:{x}\:{such}\:{that}\:{the}\:{rod}\:{doesn}'{t} \\ $$$${slip}. \\ $$$$\left[{Q}\mathrm{90331}\right] \\ $$

Answered by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

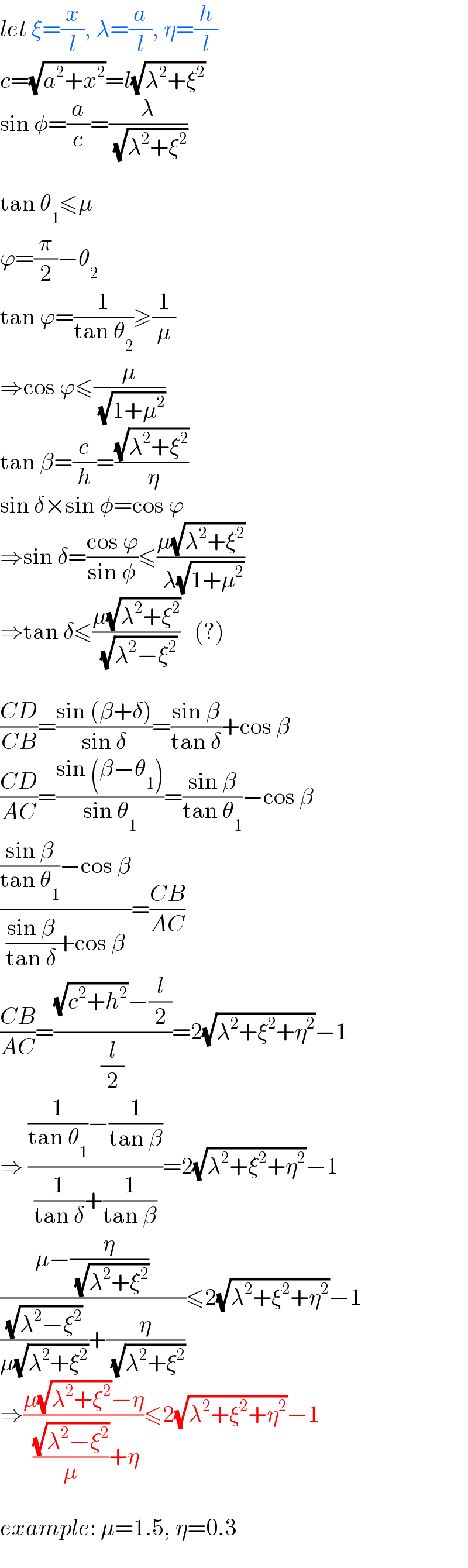
let ξ=(x/l), λ=(a/l), η=(h/l) c=(√(a^2 +x^2 ))=l(√(λ^2 +ξ^2 )) sin φ=(a/c)=(λ/( (√(λ^2 +ξ^2 )))) tan θ_1 ≤μ ϕ=(π/2)−θ_2 tan ϕ=(1/(tan θ_2 ))≥(1/μ) ⇒cos ϕ≤(μ/( (√(1+μ^2 )))) tan β=(c/h)=((√(λ^2 +ξ^2 ))/( η)) sin δ×sin φ=cos ϕ ⇒sin δ=((cos ϕ)/(sin φ))≤((μ(√(λ^2 +ξ^2 )))/( λ(√(1+μ^2 )))) ⇒tan δ≤((μ(√(λ^2 +ξ^2 )))/( (√(λ^2 −ξ^2 )))) (?) ((CD)/(CB))=((sin (β+δ))/(sin δ))=((sin β)/(tan δ))+cos β ((CD)/(AC))=((sin (β−θ_1 ))/(sin θ_1 ))=((sin β)/(tan θ_1 ))−cos β ((((sin β)/(tan θ_1 ))−cos β)/(((sin β)/(tan δ))+cos β))=((CB)/(AC)) ((CB)/(AC))=(((√(c^2 +h^2 ))−(l/2))/(l/2))=2(√(λ^2 +ξ^2 +η^2 ))−1 ⇒ (((1/(tan θ_1 ))−(1/(tan β)))/((1/(tan δ))+(1/(tan β))))=2(√(λ^2 +ξ^2 +η^2 ))−1 ((μ−(η/( (√(λ^2 +ξ^2 )))))/(((√(λ^2 −ξ^2 ))/(μ(√(λ^2 +ξ^2 ))))+(η/( (√(λ^2 +ξ^2 ))))))≤2(√(λ^2 +ξ^2 +η^2 ))−1 ⇒((μ(√(λ^2 +ξ^2 ))−η)/( ((√(λ^2 −ξ^2 ))/μ)+η))≤2(√(λ^2 +ξ^2 +η^2 ))−1 example: μ=1.5, η=0.3

$${let}\:\xi=\frac{{x}}{{l}},\:\lambda=\frac{{a}}{{l}},\:\eta=\frac{{h}}{{l}} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }={l}\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:\phi=\frac{{a}}{{c}}=\frac{\lambda}{\:\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }} \\ $$$$ \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} \leqslant\mu \\ $$$$\varphi=\frac{\pi}{\mathrm{2}}−\theta_{\mathrm{2}} \\ $$$$\mathrm{tan}\:\varphi=\frac{\mathrm{1}}{\mathrm{tan}\:\theta_{\mathrm{2}} }\geqslant\frac{\mathrm{1}}{\mu} \\ $$$$\Rightarrow\mathrm{cos}\:\varphi\leqslant\frac{\mu}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\beta=\frac{{c}}{{h}}=\frac{\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }}{\:\eta} \\ $$$$\mathrm{sin}\:\delta×\mathrm{sin}\:\phi=\mathrm{cos}\:\varphi \\ $$$$\Rightarrow\mathrm{sin}\:\delta=\frac{\mathrm{cos}\:\varphi}{\mathrm{sin}\:\phi}\leqslant\frac{\mu\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }}{\:\lambda\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{tan}\:\delta\leqslant\frac{\mu\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }}{\:\sqrt{\lambda^{\mathrm{2}} −\xi^{\mathrm{2}} }}\:\:\:\left(?\right) \\ $$$$ \\ $$$$\frac{{CD}}{{CB}}=\frac{\mathrm{sin}\:\left(\beta+\delta\right)}{\mathrm{sin}\:\delta}=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\delta}+\mathrm{cos}\:\beta \\ $$$$\frac{{CD}}{{AC}}=\frac{\mathrm{sin}\:\left(\beta−\theta_{\mathrm{1}} \right)}{\mathrm{sin}\:\theta_{\mathrm{1}} }=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\theta_{\mathrm{1}} }−\mathrm{cos}\:\beta \\ $$$$\frac{\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\theta_{\mathrm{1}} }−\mathrm{cos}\:\beta}{\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\delta}+\mathrm{cos}\:\beta}=\frac{{CB}}{{AC}} \\ $$$$\frac{{CB}}{{AC}}=\frac{\sqrt{{c}^{\mathrm{2}} +{h}^{\mathrm{2}} }−\frac{{l}}{\mathrm{2}}}{\frac{{l}}{\mathrm{2}}}=\mathrm{2}\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }−\mathrm{1} \\ $$$$\Rightarrow\:\frac{\frac{\mathrm{1}}{\mathrm{tan}\:\theta_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{tan}\:\beta}}{\frac{\mathrm{1}}{\mathrm{tan}\:\delta}+\frac{\mathrm{1}}{\mathrm{tan}\:\beta}}=\mathrm{2}\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }−\mathrm{1} \\ $$$$\frac{\mu−\frac{\eta}{\:\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }}}{\frac{\sqrt{\lambda^{\mathrm{2}} −\xi^{\mathrm{2}} }}{\mu\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }}+\frac{\eta}{\:\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }}}\leqslant\mathrm{2}\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }−\mathrm{1} \\ $$$$\Rightarrow\frac{\mu\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} }−\eta}{\:\frac{\sqrt{\lambda^{\mathrm{2}} −\xi^{\mathrm{2}} }}{\mu}+\eta}\leqslant\mathrm{2}\sqrt{\lambda^{\mathrm{2}} +\xi^{\mathrm{2}} +\eta^{\mathrm{2}} }−\mathrm{1} \\ $$$$ \\ $$$${example}:\:\mu=\mathrm{1}.\mathrm{5},\:\eta=\mathrm{0}.\mathrm{3} \\ $$

Commented by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

$${since}\:{we}\:{don}'{t}\:{have}\:{a}\:{contact}\:{surface} \\ $$$${between}\:{the}\:{rod}\:{and}\:{the}\:{step}\:{edge}\:{in}\: \\ $$$${this}\:{case},\:{i}'{m}\:{not}\:{sure}\:{if}\:{my}\:{solution} \\ $$$${is}\:{correct}.\:{comments}\:{are}\:{welcome}. \\ $$

Commented by Tawa11 last updated on 04/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply