Question Number 177446 by mr W last updated on 05/Oct/22
Commented by mr W last updated on 05/Oct/22

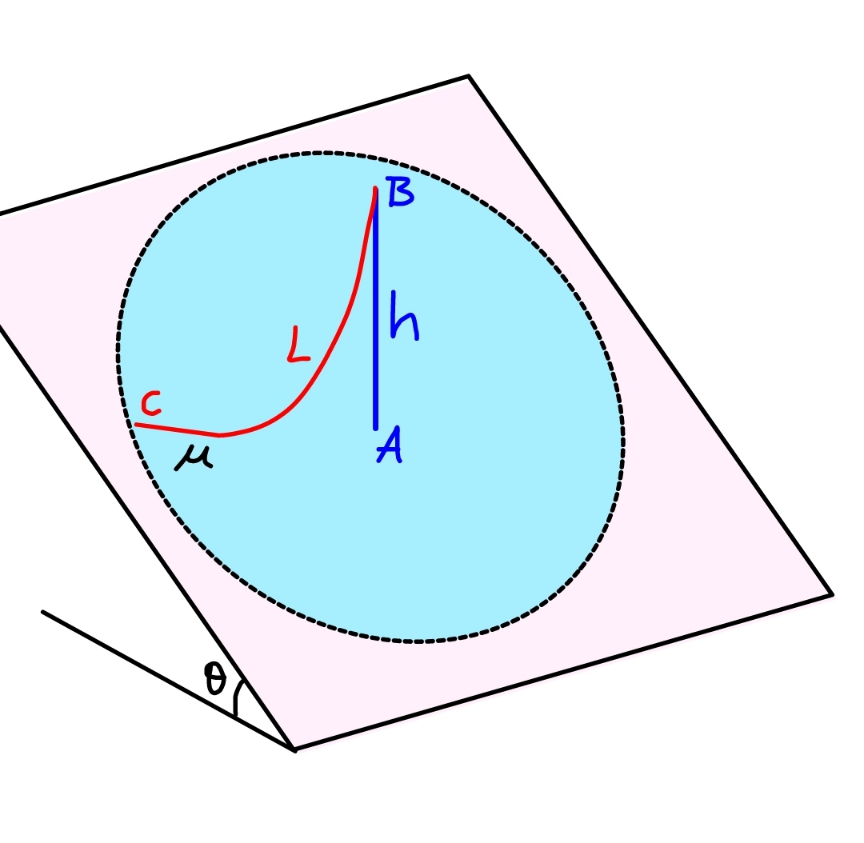
$${a}\:{rope}\:{with}\:{length}\:{L}\:{has}\:{uniform} \\ $$$${mass}.\:{one}\:{end}\:{of}\:{the}\:{rope}\:{is}\:{fixed}\:{on} \\ $$$${the}\:{top}\:{of}\:{a}\:{pole}\:{with}\:{heigth}\:{h}\:{above}\:{a} \\ $$$${inclined}\:{plane}\:\left({h}<{L}\right).\:{the}\:{other}\:{end} \\ $$$${of}\:{the}\:{rope}\:{can}\:{be}\:{freely}\:{laid}\:{on}\:{the} \\ $$$${inclined}\:{plane}.\:{the}\:{friction}\:{coefficient}\: \\ $$$${between}\:{rope}\:{and}\:{inclined}\:{plane}\:{is}\:\mu. \\ $$$${find}\:{the}\:{maximum}\:{area}\:{of}\:{the}\: \\ $$$${inclined}\:{plane}\:{which}\:{can}\:{be}\:{covered}\: \\ $$$${by}\:{the}\:{rope}. \\ $$
Answered by mr W last updated on 06/Oct/22
Commented by mr W last updated on 06/Oct/22
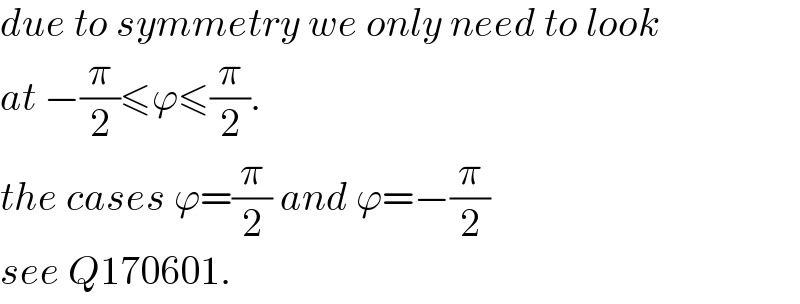
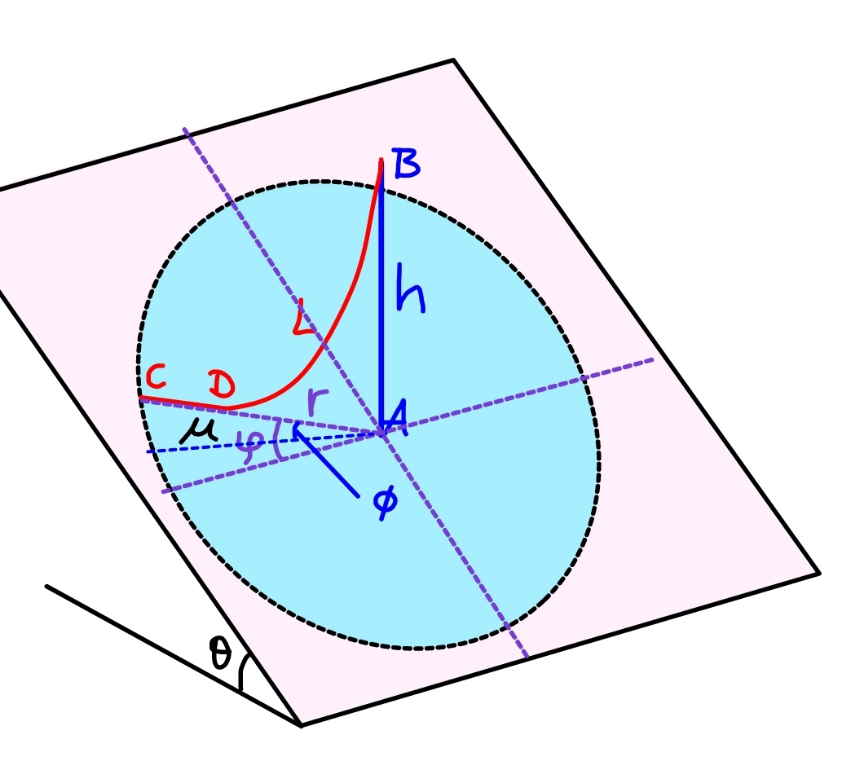
$${due}\:{to}\:{symmetry}\:{we}\:{only}\:{need}\:{to}\:{look} \\ $$$${at}\:−\frac{\pi}{\mathrm{2}}\leqslant\varphi\leqslant\frac{\pi}{\mathrm{2}}.\: \\ $$$${the}\:{cases}\:\varphi=\frac{\pi}{\mathrm{2}}\:{and}\:\varphi=−\frac{\pi}{\mathrm{2}}\: \\ $$$${see}\:{Q}\mathrm{170601}. \\ $$
Commented by mr W last updated on 06/Oct/22
Commented by mr W last updated on 07/Oct/22
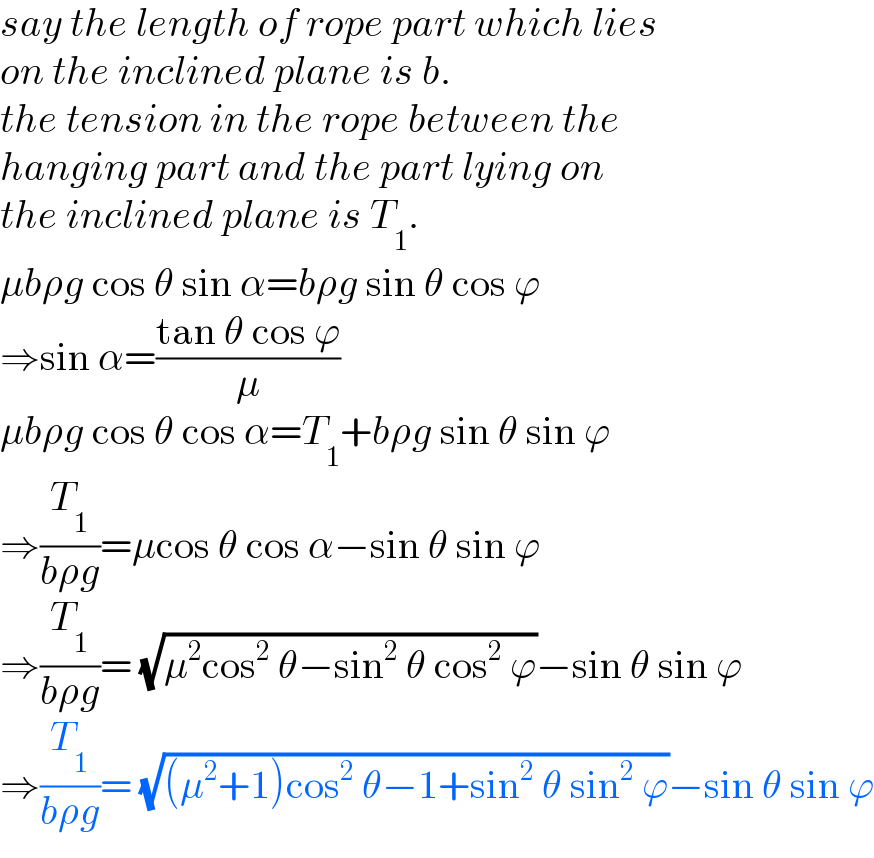
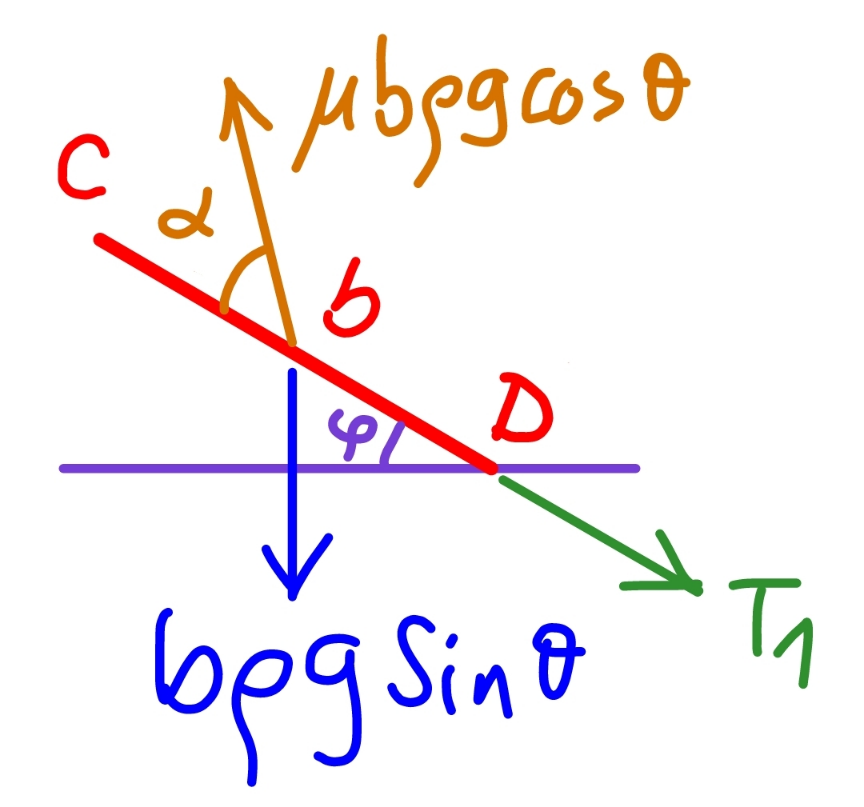
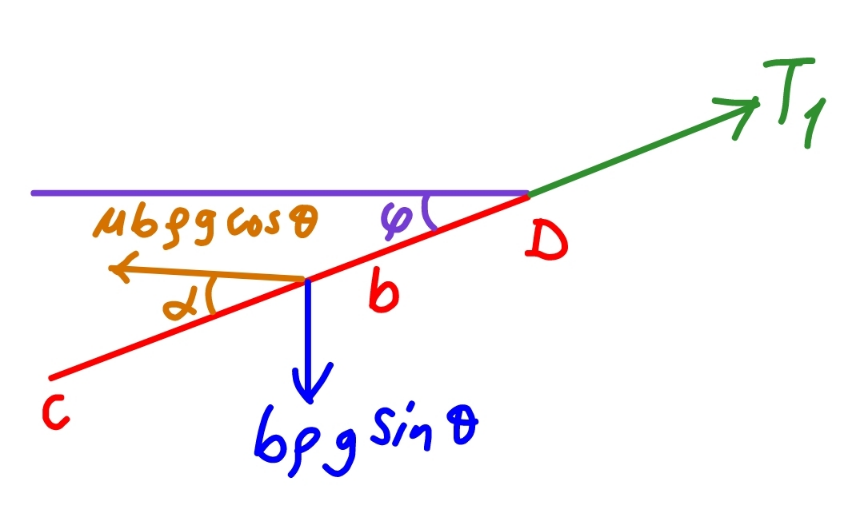
$${say}\:{the}\:{length}\:{of}\:{rope}\:{part}\:{which}\:{lies} \\ $$$${on}\:{the}\:{inclined}\:{plane}\:{is}\:{b}. \\ $$$${the}\:{tension}\:{in}\:{the}\:{rope}\:{between}\:{the} \\ $$$${hanging}\:{part}\:{and}\:{the}\:{part}\:{lying}\:{on} \\ $$$${the}\:{inclined}\:{plane}\:{is}\:{T}_{\mathrm{1}} . \\ $$$$\mu{b}\rho{g}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\alpha={b}\rho{g}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{tan}\:\theta\:\mathrm{cos}\:\varphi}{\mu} \\ $$$$\mu{b}\rho{g}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\alpha={T}_{\mathrm{1}} +{b}\rho{g}\:\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow\frac{{T}_{\mathrm{1}} }{{b}\rho{g}}=\mu\mathrm{cos}\:\theta\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow\frac{{T}_{\mathrm{1}} }{{b}\rho{g}}=\:\sqrt{\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{cos}^{\mathrm{2}} \:\varphi}−\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow\frac{{T}_{\mathrm{1}} }{{b}\rho{g}}=\:\sqrt{\left(\mu^{\mathrm{2}} +\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{sin}^{\mathrm{2}} \:\varphi}−\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$
Commented by mr W last updated on 07/Oct/22
![let η=(h/L), ξ=(b/L) sin φ=sin ϕ sin θ=λ, say a=(T_0 /(ρg))=((T_1 cos φ)/(ρg)) =b cos φ( (√((1+μ^2 )cos^2 θ−1+λ^2 ))−λ) =ξL(√(1−λ^2 ))((√((μ^2 +1)cos^2 θ−1+λ^2 ))−λ) let δ= (√((μ^2 +1)cos^2 θ−1+λ^2 ))−λ ⇒a=ξLδ (√(1−λ^2 )) eqn. of catenary in xy−system: y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) at point D: y′=sinh (d_1 /a)=tan φ ⇒(d_1 /a)=sinh^(−1) (tan φ)=sinh^(−1) (λ/( (√(1−λ^2 )))) h_2 =a cosh (d_1 /a)=a cosh (sinh^(−1) (λ/( (√(1−λ^2 ))))) =a (√(1+((λ/( (√(1−λ^2 )))))^2 ))=(a/( (√(1−λ^2 )))) s_1 =a tan φ=((aλ)/( (√(1−λ^2 )))) at point B: h_3 =a cosh (d_2 /a) s_2 =a sinh (d_2 /a) h_1 =h−h_3 (h_1 /a)=(h/a)−(h_3 /a) h_1 +h_2 =(d_1 +d_2 )tan φ ((h/a)−(h_3 /a)+(h_2 /a))((√(1−λ^2 ))/λ)=(d_1 /a)+(d_2 /a) ((h/a)−cosh (d_2 /a)+ (1/( (√(1−λ^2 )))))((√(1−λ^2 ))/λ)=sinh^(−1) (λ/( (√(1−λ^2 ))))+(d_2 /a) ((h/a)−cosh (d_2 /a))((√(1−λ^2 ))/λ)+ (1/( λ))=sinh^(−1) (λ/( (√(1−λ^2 ))))+(d_2 /a) (d_2 /a)+((√(1−λ^2 ))/λ) cosh (d_2 /a)=(1/λ)(((h(√(1−λ^2 )))/a)+1)−sinh^(−1) (λ/( (√(1−λ^2 )))) ⇒ λ((d_2 /a))+(√(1−λ^2 )) cosh (d_2 /a)=(η/(ξδ))+1−λ sinh^(−1) (λ/( (√(1−λ^2 )))) ...(i) s_1 +s_2 =L−b (s_1 /a)+(s_2 /a)=((L−b)/a) (λ/( (√(1−λ^2 ))))+sinh (d_2 /a)=((1−ξ)/(ξδ (√(1−λ^2 )))) sinh (d_2 /a)=(1/( (√(1−λ^2 ))))(((1−ξ)/(ξδ))−λ) ⇒(d_2 /a)=sinh^(−1) [ (1/( (√(1−λ^2 ))))(((1−ξ)/(ξδ))−λ)] ...(ii) insert (ii) into (i) we get an equation for solving ξ. r=AC=b+((d_1 +d_2 )/(cos φ)) =b+(a/(cos φ))((d_1 /a)+(d_2 /a)) =ξL+ξLδ{sinh^(−1) (λ/( (√(1−λ^2 ))))+sinh^(−1) [(1/( (√(1−λ^2 ))))(((1−ξ)/( ξδ))−λ) ]} ⇒ (r/L) =ξ+ξδ{sinh^(−1) (λ/( (√(1−λ^2 ))))+sinh^(−1) [(1/( (√(1−λ^2 )))) (((1−ξ)/( ξδ))−λ) ]} examples: μ=1.5, θ=30°, η=(h/L)=(3/5)=0.6, ϕ=0° ⇒ξ=(b/L)=0.1975, (r/L)=0.6556 ϕ=30° ⇒ξ=(b/L)=0.2556, (r/L)=0.7583 ϕ=60° ⇒ξ=(b/L)=0.3092, (r/L)=0.8551 ϕ=90° ⇒ξ=(b/L)=0.3320^(∗)) , (r/L)=0.8975 ∗) the same result as in Q170601](https://www.tinkutara.com/question/Q177531.png)
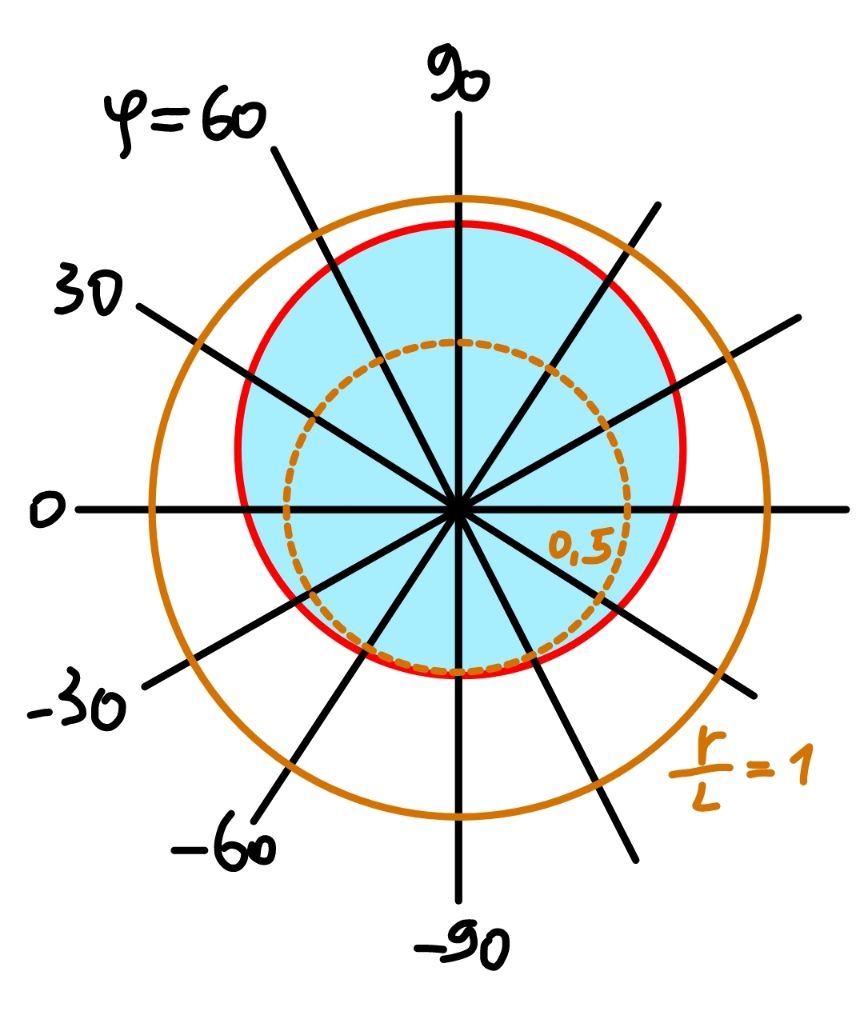
$${let}\:\eta=\frac{{h}}{{L}},\:\xi=\frac{{b}}{{L}} \\ $$$$\mathrm{sin}\:\phi=\mathrm{sin}\:\varphi\:\mathrm{sin}\:\theta=\lambda,\:{say} \\ $$$${a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{{T}_{\mathrm{1}} \mathrm{cos}\:\phi}{\rho{g}} \\ $$$$\:\:={b}\:\mathrm{cos}\:\phi\left(\:\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\lambda^{\mathrm{2}} }−\lambda\right) \\ $$$$\:\:=\xi{L}\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\left(\sqrt{\left(\mu^{\mathrm{2}} +\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\lambda^{\mathrm{2}} }−\lambda\right) \\ $$$${let}\:\delta=\:\sqrt{\left(\mu^{\mathrm{2}} +\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\lambda^{\mathrm{2}} }−\lambda \\ $$$$\Rightarrow{a}=\xi{L}\delta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$ \\ $$$${eqn}.\:{of}\:{catenary}\:{in}\:{xy}−{system}: \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$$ \\ $$$${at}\:{point}\:{D}: \\ $$$${y}'=\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{tan}\:\phi \\ $$$$\Rightarrow\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\phi\right)=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$${h}_{\mathrm{2}} ={a}\:\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} }{{a}}={a}\:\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right) \\ $$$$\:\:\:\:\:={a}\:\sqrt{\mathrm{1}+\left(\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right)^{\mathrm{2}} }=\frac{{a}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$${s}_{\mathrm{1}} ={a}\:\mathrm{tan}\:\phi=\frac{{a}\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$ \\ $$$${at}\:{point}\:{B}: \\ $$$${h}_{\mathrm{3}} ={a}\:\mathrm{cosh}\:\frac{{d}_{\mathrm{2}} }{{a}} \\ $$$${s}_{\mathrm{2}} ={a}\:\mathrm{sinh}\:\frac{{d}_{\mathrm{2}} }{{a}} \\ $$$${h}_{\mathrm{1}} ={h}−{h}_{\mathrm{3}} \\ $$$$\frac{{h}_{\mathrm{1}} }{{a}}=\frac{{h}}{{a}}−\frac{{h}_{\mathrm{3}} }{{a}} \\ $$$${h}_{\mathrm{1}} +{h}_{\mathrm{2}} =\left({d}_{\mathrm{1}} +{d}_{\mathrm{2}} \right)\mathrm{tan}\:\phi \\ $$$$\left(\frac{{h}}{{a}}−\frac{{h}_{\mathrm{3}} }{{a}}+\frac{{h}_{\mathrm{2}} }{{a}}\right)\frac{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{\lambda}=\frac{{d}_{\mathrm{1}} }{{a}}+\frac{{d}_{\mathrm{2}} }{{a}} \\ $$$$\left(\frac{{h}}{{a}}−\mathrm{cosh}\:\frac{{d}_{\mathrm{2}} }{{a}}+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right)\frac{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{\lambda}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\frac{{d}_{\mathrm{2}} }{{a}} \\ $$$$\left(\frac{{h}}{{a}}−\mathrm{cosh}\:\frac{{d}_{\mathrm{2}} }{{a}}\right)\frac{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{\lambda}+\:\frac{\mathrm{1}}{\:\lambda}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\frac{{d}_{\mathrm{2}} }{{a}} \\ $$$$\frac{{d}_{\mathrm{2}} }{{a}}+\frac{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{\lambda}\:\mathrm{cosh}\:\frac{{d}_{\mathrm{2}} }{{a}}=\frac{\mathrm{1}}{\lambda}\left(\frac{{h}\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}{{a}}+\mathrm{1}\right)−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\lambda\left(\frac{{d}_{\mathrm{2}} }{{a}}\right)+\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\:\mathrm{cosh}\:\frac{{d}_{\mathrm{2}} }{{a}}=\frac{\eta}{\xi\delta}+\mathrm{1}−\lambda\:\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${s}_{\mathrm{1}} +{s}_{\mathrm{2}} ={L}−{b} \\ $$$$\frac{{s}_{\mathrm{1}} }{{a}}+\frac{{s}_{\mathrm{2}} }{{a}}=\frac{{L}−{b}}{{a}} \\ $$$$\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\mathrm{sinh}\:\frac{{d}_{\mathrm{2}} }{{a}}=\frac{\mathrm{1}−\xi}{\xi\delta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$\mathrm{sinh}\:\frac{{d}_{\mathrm{2}} }{{a}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{1}−\xi}{\xi\delta}−\lambda\right) \\ $$$$\Rightarrow\frac{{d}_{\mathrm{2}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \left[\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{1}−\xi}{\xi\delta}−\lambda\right)\right]\:\:\:\:…\left({ii}\right) \\ $$$${insert}\:\left({ii}\right)\:{into}\:\left({i}\right)\:{we}\:{get}\:{an}\:{equation} \\ $$$${for}\:{solving}\:\xi. \\ $$$$ \\ $$$${r}={AC}={b}+\frac{{d}_{\mathrm{1}} +{d}_{\mathrm{2}} }{\mathrm{cos}\:\phi} \\ $$$$\:\:={b}+\frac{{a}}{\mathrm{cos}\:\phi}\left(\frac{{d}_{\mathrm{1}} }{{a}}+\frac{{d}_{\mathrm{2}} }{{a}}\right) \\ $$$$\:\:=\xi{L}+\xi{L}\delta\left\{\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\mathrm{sinh}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{1}−\xi}{\:\xi\delta}−\lambda\right)\:\right]\right\} \\ $$$$\Rightarrow\:\frac{{r}}{{L}}\:=\xi+\xi\delta\left\{\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\mathrm{sinh}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\:\left(\frac{\mathrm{1}−\xi}{\:\xi\delta}−\lambda\right)\:\right]\right\} \\ $$$$ \\ $$$$\boldsymbol{{examples}}: \\ $$$$\mu=\mathrm{1}.\mathrm{5},\:\theta=\mathrm{30}°,\:\eta=\frac{{h}}{{L}}=\frac{\mathrm{3}}{\mathrm{5}}=\mathrm{0}.\mathrm{6}, \\ $$$$\varphi=\mathrm{0}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{1975},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{6556} \\ $$$$\varphi=\mathrm{30}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{2556},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{7583} \\ $$$$\varphi=\mathrm{60}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{3092},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{8551} \\ $$$$\varphi=\mathrm{90}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{3320}^{\left.\ast\right)} ,\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{8975} \\ $$$$ \\ $$$$\left.\ast\right)\:{the}\:{same}\:{result}\:{as}\:{in}\:{Q}\mathrm{170601} \\ $$
Commented by mr W last updated on 06/Oct/22
Commented by mr W last updated on 07/Oct/22
Commented by mr W last updated on 07/Oct/22
Commented by mr W last updated on 07/Oct/22
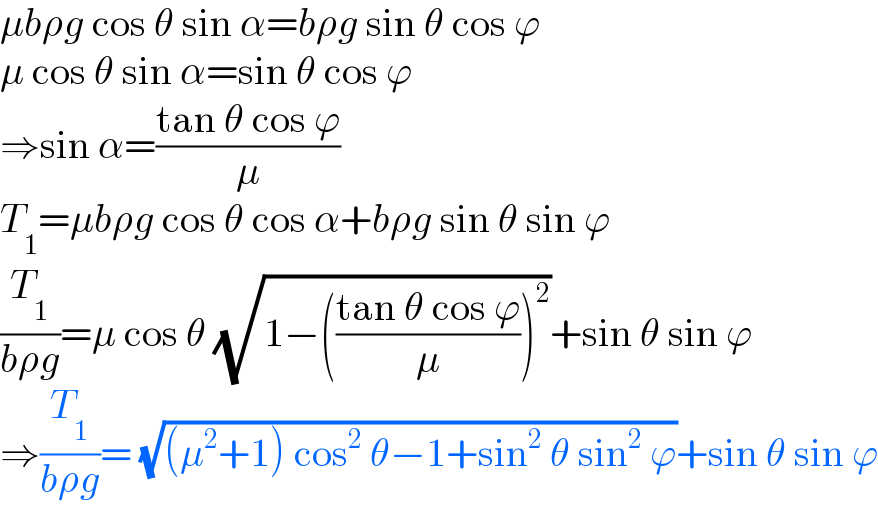
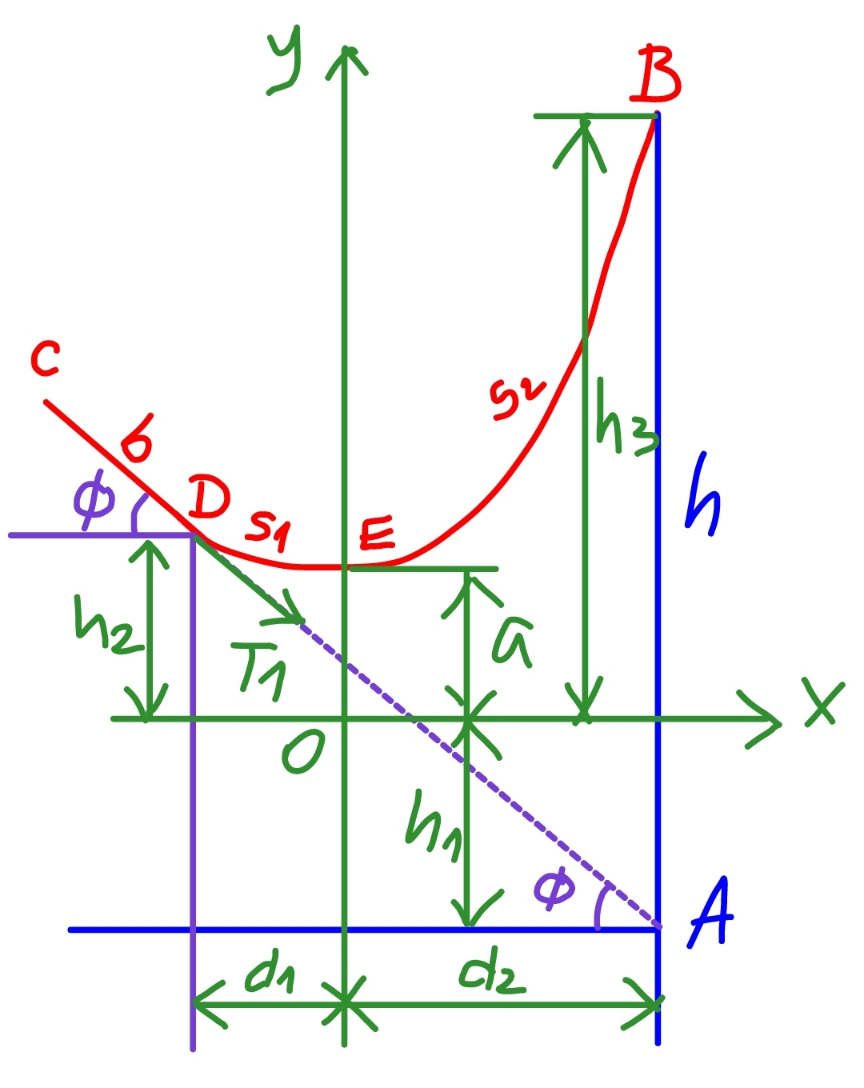
$$\mu{b}\rho{g}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\alpha={b}\rho{g}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi \\ $$$$\mu\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\alpha=\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{tan}\:\theta\:\mathrm{cos}\:\varphi}{\mu} \\ $$$${T}_{\mathrm{1}} =\mu{b}\rho{g}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\alpha+{b}\rho{g}\:\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$\frac{{T}_{\mathrm{1}} }{{b}\rho{g}}=\mu\:\mathrm{cos}\:\theta\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{tan}\:\theta\:\mathrm{cos}\:\varphi}{\mu}\right)^{\mathrm{2}} }+\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow\frac{{T}_{\mathrm{1}} }{{b}\rho{g}}=\:\sqrt{\left(\mu^{\mathrm{2}} +\mathrm{1}\right)\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{sin}^{\mathrm{2}} \:\varphi}+\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi \\ $$
Commented by mr W last updated on 07/Oct/22
Commented by mr W last updated on 07/Oct/22
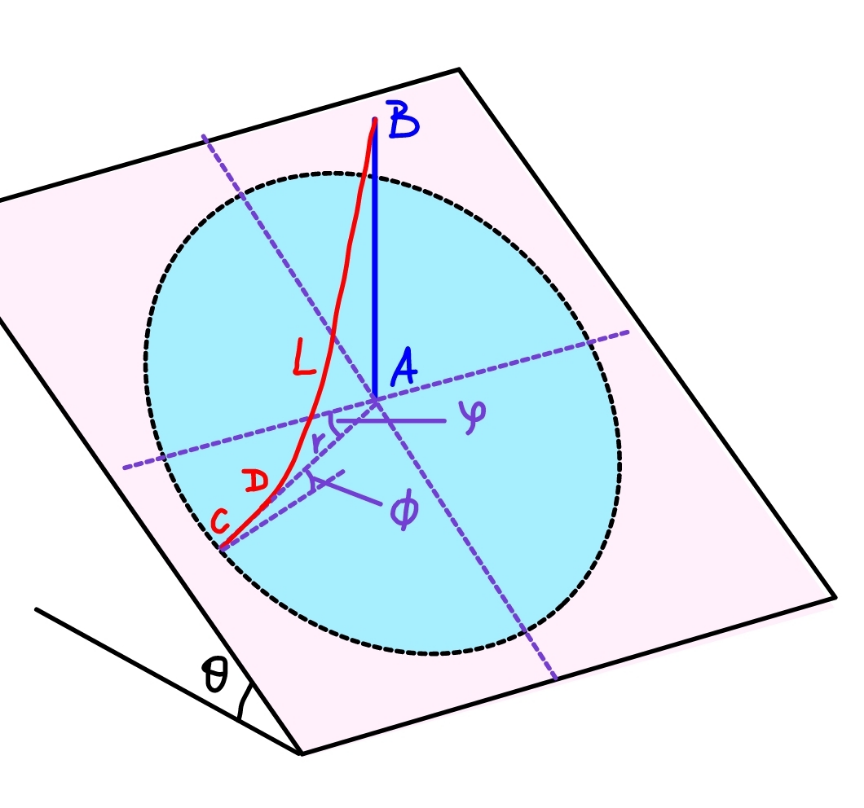
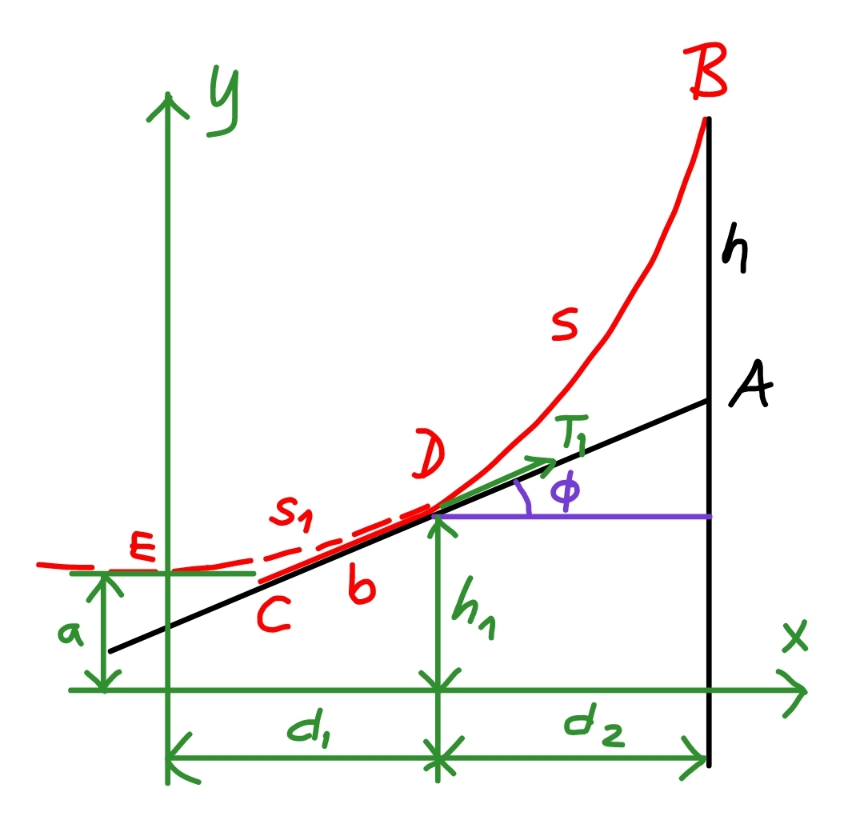
![let η=(h/L), ξ=(b/L) sin φ=sin ϕ sin θ=λ, say a=(T_0 /(ρg))=((T_1 cos φ)/(ρg)) =b cos φ( (√((1+μ^2 )cos^2 θ−1+λ^2 ))+λ) =ξL(√(1−λ^2 ))((√((μ^2 +1)cos^2 θ−1+λ^2 ))+λ) let δ= (√((μ^2 +1)cos^2 θ−1+λ^2 ))+λ ⇒a=ξLδ (√(1−λ^2 )) eqn. of catenary in xy−system: y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) at point D: y′=sinh (d_1 /a)=tan φ ⇒(d_1 /a)=sinh^(−1) (tan φ)=sinh^(−1) (λ/( (√(1−λ^2 )))) h_1 =a cosh (d_1 /a)=a cosh (sinh^(−1) (λ/( (√(1−λ^2 ))))) =a (√(1+((λ/( (√(1−λ^2 )))))^2 ))=(a/( (√(1−λ^2 )))) s_1 =a tan φ=((aλ)/( (√(1−λ^2 )))) at point B: h_1 +d_2 tan φ+h=a cosh ((d_1 +d_2 )/a) (h_1 /a)+(d_2 /a) tan φ+(h/a)=cosh ((d_1 +d_2 )/a) (1/( (√(1−λ^2 ))))+(η/(ξδ (√(1−λ^2 ))))=cosh ((d_2 /a)+sinh^(−1) (λ/( (√(1−λ^2 )))))−(d_2 /a)×(λ/( (√(1−λ^2 )))) ⇒(√(1−λ^2 ))cosh ((d_2 /a)+sinh^(−1) (λ/( (√(1−λ^2 )))))−λ((d_2 /a))=1+(η/(ξδ )) ...(i) s_1 +s=a sinh ((d_1 +d_2 )/a) (s_1 /a)+((L−b)/a)=sinh ((d_2 /a)+(d_1 /a)) (λ/( (√(1−λ^2 ))))+((1−ξ)/(ξδ (√(1−λ^2 ))))=sinh ((d_2 /a)+sinh^(−1) (λ/( (√(1−λ^2 ))))) ⇒(d_2 /a)=sinh^− [(1/( (√(1−λ^2 ))))(((1−ξ)/(ξδ))+λ)]−sinh^(−1) (λ/( (√(1−λ^2 )))) ...(ii) insert (ii) into (i) we get an equation for solving ξ. r=AC=b+(d_2 /(cos φ)) =b+(a/(cos φ))×(d_2 /a) =ξL+ξLδ{sinh^(−1) [(1/( (√(1−λ^2 ))))(((1−ξ)/( ξδ))+λ) ]−sinh^(−1) (λ/( (√(1−λ^2 ))))} ⇒(r/L)=ξ+ξδ{sinh^(−1) [(1/( (√(1−λ^2 ))))(((1−ξ)/( ξδ))+λ) ]−sinh^(−1) (λ/( (√(1−λ^2 ))))} examples: μ=1.5, θ=30°, η=(h/L)=(3/5)=0.6, ϕ=0° ⇒ξ=(b/L)=0.1975, (r/L)=0.6556 ϕ=30° ⇒ξ=(b/L)=0.1521, (r/L)=0.5733 ϕ=60° ⇒ξ=(b/L)=0.1257, (r/L)=0.5225 ϕ=90° ⇒ξ=(b/L)=0.1172, (r/L)=0.5053](https://www.tinkutara.com/question/Q177667.png)
$${let}\:\eta=\frac{{h}}{{L}},\:\xi=\frac{{b}}{{L}} \\ $$$$\mathrm{sin}\:\phi=\mathrm{sin}\:\varphi\:\mathrm{sin}\:\theta=\lambda,\:{say} \\ $$$${a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{{T}_{\mathrm{1}} \mathrm{cos}\:\phi}{\rho{g}} \\ $$$$\:\:={b}\:\mathrm{cos}\:\phi\left(\:\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\lambda^{\mathrm{2}} }+\lambda\right) \\ $$$$\:\:=\xi{L}\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\left(\sqrt{\left(\mu^{\mathrm{2}} +\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\lambda^{\mathrm{2}} }+\lambda\right) \\ $$$${let}\:\delta=\:\sqrt{\left(\mu^{\mathrm{2}} +\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}+\lambda^{\mathrm{2}} }+\lambda \\ $$$$\Rightarrow{a}=\xi{L}\delta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$ \\ $$$${eqn}.\:{of}\:{catenary}\:{in}\:{xy}−{system}: \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$$ \\ $$$${at}\:{point}\:{D}: \\ $$$${y}'=\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{tan}\:\phi \\ $$$$\Rightarrow\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\phi\right)=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$${h}_{\mathrm{1}} ={a}\:\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} }{{a}}={a}\:\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right) \\ $$$$\:\:\:\:\:={a}\:\sqrt{\mathrm{1}+\left(\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right)^{\mathrm{2}} }=\frac{{a}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$${s}_{\mathrm{1}} ={a}\:\mathrm{tan}\:\phi=\frac{{a}\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$ \\ $$$${at}\:{point}\:{B}: \\ $$$${h}_{\mathrm{1}} +{d}_{\mathrm{2}} \:\mathrm{tan}\:\phi+{h}={a}\:\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} +{d}_{\mathrm{2}} }{{a}} \\ $$$$\frac{{h}_{\mathrm{1}} }{{a}}+\frac{{d}_{\mathrm{2}} }{{a}}\:\mathrm{tan}\:\phi+\frac{{h}}{{a}}=\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} +{d}_{\mathrm{2}} }{{a}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\frac{\eta}{\xi\delta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}=\mathrm{cosh}\:\left(\frac{{d}_{\mathrm{2}} }{{a}}+\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right)−\frac{{d}_{\mathrm{2}} }{{a}}×\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$\Rightarrow\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \:}\mathrm{cosh}\:\left(\frac{{d}_{\mathrm{2}} }{{a}}+\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right)−\lambda\left(\frac{{d}_{\mathrm{2}} }{{a}}\right)=\mathrm{1}+\frac{\eta}{\xi\delta\:}\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${s}_{\mathrm{1}} +{s}={a}\:\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} +{d}_{\mathrm{2}} }{{a}} \\ $$$$\frac{{s}_{\mathrm{1}} }{{a}}+\frac{{L}−{b}}{{a}}=\mathrm{sinh}\:\left(\frac{{d}_{\mathrm{2}} }{{a}}+\frac{{d}_{\mathrm{1}} }{{a}}\right) \\ $$$$\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}+\frac{\mathrm{1}−\xi}{\xi\delta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}=\mathrm{sinh}\:\left(\frac{{d}_{\mathrm{2}} }{{a}}+\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow\frac{{d}_{\mathrm{2}} }{{a}}=\mathrm{sinh}^{−} \:\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{1}−\xi}{\xi\delta}+\lambda\right)\right]−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\:\:\:\:…\left({ii}\right) \\ $$$${insert}\:\left({ii}\right)\:{into}\:\left({i}\right)\:{we}\:{get}\:{an}\:{equation} \\ $$$${for}\:{solving}\:\xi. \\ $$$$ \\ $$$${r}={AC}={b}+\frac{{d}_{\mathrm{2}} }{\mathrm{cos}\:\phi} \\ $$$$\:\:={b}+\frac{{a}}{\mathrm{cos}\:\phi}×\frac{{d}_{\mathrm{2}} }{{a}} \\ $$$$\:\:=\xi{L}+\xi{L}\delta\left\{\mathrm{sinh}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{1}−\xi}{\:\xi\delta}+\lambda\right)\:\right]−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right\} \\ $$$$\Rightarrow\frac{{r}}{{L}}=\xi+\xi\delta\left\{\mathrm{sinh}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{1}−\xi}{\:\xi\delta}+\lambda\right)\:\right]−\mathrm{sinh}^{−\mathrm{1}} \:\frac{\lambda}{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}\right\} \\ $$$$ \\ $$$$\boldsymbol{{examples}}: \\ $$$$\mu=\mathrm{1}.\mathrm{5},\:\theta=\mathrm{30}°,\:\eta=\frac{{h}}{{L}}=\frac{\mathrm{3}}{\mathrm{5}}=\mathrm{0}.\mathrm{6}, \\ $$$$\varphi=\mathrm{0}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{1975},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{6556} \\ $$$$\varphi=\mathrm{30}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{1521},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{5733} \\ $$$$\varphi=\mathrm{60}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{1257},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{5225} \\ $$$$\varphi=\mathrm{90}°\:\Rightarrow\xi=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{1172},\:\frac{{r}}{{L}}=\mathrm{0}.\mathrm{5053} \\ $$
Commented by mr W last updated on 08/Oct/22