Question Number 177541 by peter frank last updated on 06/Oct/22

Commented by cortano1 last updated on 07/Oct/22
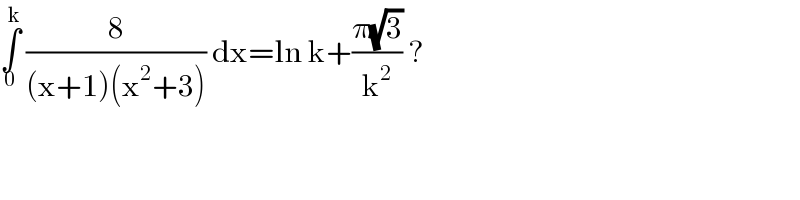
$$\underset{\mathrm{0}} {\overset{\mathrm{k}} {\int}}\:\frac{\mathrm{8}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)}\:\mathrm{dx}=\mathrm{ln}\:\mathrm{k}+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{k}^{\mathrm{2}} }\:? \\ $$
Commented by peter frank last updated on 07/Oct/22
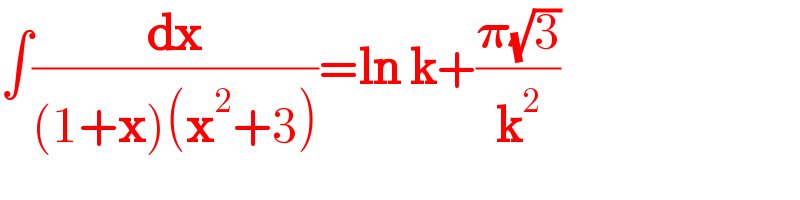
$$\int\frac{\boldsymbol{\mathrm{dx}}}{\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{3}\right)}=\boldsymbol{\mathrm{ln}}\:\boldsymbol{\mathrm{k}}+\frac{\boldsymbol{\pi}\sqrt{\mathrm{3}}}{\boldsymbol{\mathrm{k}}^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 07/Oct/22

$${an}\:{indefinite}\:{integral}\:{is}\:{not}\:{a}\:{value}, \\ $$$${but}\:{a}\:{function}!\:{you}\:{can}'{t}\:{determine}\:{k}. \\ $$$${therefore}\:{the}\:{question}\:{must}\:{be}\:{an} \\ $$$${definite}\:{integral}\:{with}\:{start}\:{and}\:{end} \\ $$$${value}! \\ $$
