Menu Close

Question-177542

Tinku Tara 0 Comments
Pin




Question Number 177542 by peter frank last updated on 06/Oct/22
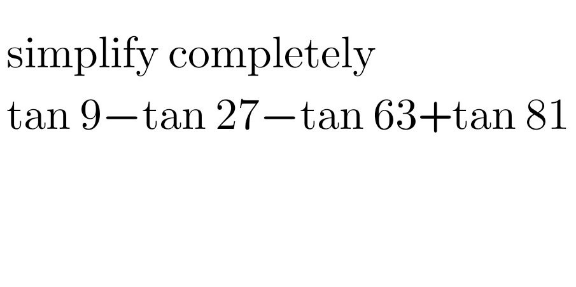
Answered by Frix last updated on 07/Oct/22
9°=x 27°=3x tan (90°−x) =(1/(tan x)) 81°=90°−9° 63°=90°−27° tan x =((sin x)/(cos x)) tan 3x =((tan^3 x −3tan x)/(3tan^2 x −1))=(((sin^2 x −3cos^2 x)sin x)/((3sin^2 x −cos^2 x)cos x)) tan x +(1/(tan x))−(tan 3x +(1/(tan 3x)))= =((2(sin^2 x −2cos x sin x −cos^2 x)(sin^2 x +2cos x sin x −cos^2 x))/(cos x sin x (sin^2 x −3cos^2 x)(3sin^2 x −cos^2 x))) sin^2 x =((1−cos 2x)/2) cos^2 x =((1+cos 2x)/2) cos x sin x =((sin 2x)/2) now we have ((4(cos^2 2x −sin^2 2x))/((4cos^2 2x −1)sin 2x))=((4(2cos^2 2x −1))/((4cos^2 2x−1)sin 2x))= =((4cos 4x)/(sin 6x)) but x=9° ((4cos 36°)/(sin 54°)) but sin (90°−x)=cos x ((4cos 36°)/(cos 36°))=4
$$\mathrm{9}°={x} \\ $$$$\mathrm{27}°=\mathrm{3}{x} \\ $$$$\mathrm{tan}\:\left(\mathrm{90}°−{x}\right)\:=\frac{\mathrm{1}}{\mathrm{tan}\:{x}} \\ $$$$\mathrm{81}°=\mathrm{90}°−\mathrm{9}° \\ $$$$\mathrm{63}°=\mathrm{90}°−\mathrm{27}° \\ $$$$\mathrm{tan}\:{x}\:=\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}} \\ $$$$\mathrm{tan}\:\mathrm{3}{x}\:=\frac{\mathrm{tan}^{\mathrm{3}} \:{x}\:−\mathrm{3tan}\:{x}}{\mathrm{3tan}^{\mathrm{2}} \:{x}\:−\mathrm{1}}=\frac{\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:−\mathrm{3cos}^{\mathrm{2}} \:{x}\right)\mathrm{sin}\:{x}}{\left(\mathrm{3sin}^{\mathrm{2}} \:{x}\:−\mathrm{cos}^{\mathrm{2}} \:{x}\right)\mathrm{cos}\:{x}} \\ $$$$\mathrm{tan}\:{x}\:+\frac{\mathrm{1}}{\mathrm{tan}\:{x}}−\left(\mathrm{tan}\:\mathrm{3}{x}\:+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{3}{x}}\right)= \\ $$$$=\frac{\mathrm{2}\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:−\mathrm{2cos}\:{x}\:\mathrm{sin}\:{x}\:−\mathrm{cos}^{\mathrm{2}} \:{x}\right)\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:+\mathrm{2cos}\:{x}\:\mathrm{sin}\:{x}\:−\mathrm{cos}^{\mathrm{2}} \:{x}\right)}{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}\:\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:−\mathrm{3cos}^{\mathrm{2}} \:{x}\right)\left(\mathrm{3sin}^{\mathrm{2}} \:{x}\:−\mathrm{cos}^{\mathrm{2}} \:{x}\right)} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}\:=\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{4}\left(\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}\:−\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}\right)}{\left(\mathrm{4cos}^{\mathrm{2}} \:\mathrm{2}{x}\:−\mathrm{1}\right)\mathrm{sin}\:\mathrm{2}{x}}=\frac{\mathrm{4}\left(\mathrm{2cos}^{\mathrm{2}} \:\mathrm{2}{x}\:−\mathrm{1}\right)}{\left(\mathrm{4cos}^{\mathrm{2}} \:\mathrm{2}{x}−\mathrm{1}\right)\mathrm{sin}\:\mathrm{2}{x}}= \\ $$$$=\frac{\mathrm{4cos}\:\mathrm{4}{x}}{\mathrm{sin}\:\mathrm{6}{x}} \\ $$$$\mathrm{but}\:{x}=\mathrm{9}° \\ $$$$\frac{\mathrm{4cos}\:\mathrm{36}°}{\mathrm{sin}\:\mathrm{54}°} \\ $$$$\mathrm{but}\:\mathrm{sin}\:\left(\mathrm{90}°−{x}\right)=\mathrm{cos}\:{x} \\ $$$$\frac{\mathrm{4cos}\:\mathrm{36}°}{\mathrm{cos}\:\mathrm{36}°}=\mathrm{4} \\ $$
Commented by peter frank last updated on 07/Oct/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Ar Brandon last updated on 07/Oct/22
T=tan9°−tan27°−tan63°+tan81° =(tan9°+(1/(tan9°)))−(tan27°+(1/(tan27°))) =((tan^2 9°+1)/(tan9°))−((tan^2 27°+1)/(tan27°))=((sec^2 9°)/(tan9°))−((sec^2 27°)/(tan27°)) =(1/(sin9°cos9°))−(1/(sin27°cos27°))=(2/(sin18°))−(2/(sin54°)) =((2(sin54°−sin18°))/(sin18°sin54°))=((4sin18°cos36°)/(sin18°sin54°)) =((4sin18°sin54°)/(sin18°sin54°))=4
$${T}=\mathrm{tan9}°−\mathrm{tan27}°−\mathrm{tan63}°+\mathrm{tan81}° \\ $$$$\:\:\:=\left(\mathrm{tan9}°+\frac{\mathrm{1}}{\mathrm{tan9}°}\right)−\left(\mathrm{tan27}°+\frac{\mathrm{1}}{\mathrm{tan27}°}\right) \\ $$$$\:\:\:=\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{9}°+\mathrm{1}}{\mathrm{tan9}°}−\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{27}°+\mathrm{1}}{\mathrm{tan27}°}=\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{9}°}{\mathrm{tan9}°}−\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{27}°}{\mathrm{tan27}°} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{sin9}°\mathrm{cos9}°}−\frac{\mathrm{1}}{\mathrm{sin27}°\mathrm{cos27}°}=\frac{\mathrm{2}}{\mathrm{sin18}°}−\frac{\mathrm{2}}{\mathrm{sin54}°} \\ $$$$\:\:\:=\frac{\mathrm{2}\left(\mathrm{sin54}°−\mathrm{sin18}°\right)}{\mathrm{sin18}°\mathrm{sin54}°}=\frac{\mathrm{4sin18}°\mathrm{cos36}°}{\mathrm{sin18}°\mathrm{sin54}°} \\ $$$$\:\:\:=\frac{\mathrm{4sin18}°\mathrm{sin54}°}{\mathrm{sin18}°\mathrm{sin54}°}=\mathrm{4} \\ $$
Commented by peter frank last updated on 07/Oct/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Frix last updated on 07/Oct/22
or: tan 9° +tan 81° =tan 9° +(1/(tan 9°))= [(s/c)+(c/s)=((s^2 +c^2 )/(cs))=(1/(cs))] =(1/(cos 9° sin 9°)) similar −(tan 27° +tan 63°)=−(2/(sin 54°))=−(2/(sin (6×9°)))= [sin 6x =2cos x sin x (3−16cos^2 x sin^2 x) =(1/(cos 9° sin 9° (16cos^2 9° sin^2 9° −3))) (1/(cos 9° sin 9°))+(1/(cos 9° sin 9° (16cos^2 9° sin^2 9° −3)))= =((2(1−8cos^2 9° sin^2 9°))/(cos 9° sin 9° (3−16cos^2 9° sin^2 9°)))= =((4cos 36°)/(sin 54°))=4
$$\mathrm{or}: \\ $$$$\mathrm{tan}\:\mathrm{9}°\:+\mathrm{tan}\:\mathrm{81}°\:=\mathrm{tan}\:\mathrm{9}°\:+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{9}°}= \\ $$$$\left[\frac{\mathrm{s}}{\mathrm{c}}+\frac{\mathrm{c}}{\mathrm{s}}=\frac{\mathrm{s}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} }{\mathrm{cs}}=\frac{\mathrm{1}}{\mathrm{cs}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{9}°\:\mathrm{sin}\:\mathrm{9}°} \\ $$$$\mathrm{similar} \\ $$$$−\left(\mathrm{tan}\:\mathrm{27}°\:+\mathrm{tan}\:\mathrm{63}°\right)=−\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{54}°}=−\frac{\mathrm{2}}{\mathrm{sin}\:\left(\mathrm{6}×\mathrm{9}°\right)}= \\ $$$$\left[\mathrm{sin}\:\mathrm{6}{x}\:=\mathrm{2cos}\:{x}\:\mathrm{sin}\:{x}\:\left(\mathrm{3}−\mathrm{16cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{9}°\:\mathrm{sin}\:\mathrm{9}°\:\left(\mathrm{16cos}^{\mathrm{2}} \:\mathrm{9}°\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{9}°\:−\mathrm{3}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{9}°\:\mathrm{sin}\:\mathrm{9}°}+\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{9}°\:\mathrm{sin}\:\mathrm{9}°\:\left(\mathrm{16cos}^{\mathrm{2}} \:\mathrm{9}°\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{9}°\:−\mathrm{3}\right)}= \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{8cos}^{\mathrm{2}} \:\mathrm{9}°\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{9}°\right)}{\mathrm{cos}\:\mathrm{9}°\:\mathrm{sin}\:\mathrm{9}°\:\left(\mathrm{3}−\mathrm{16cos}^{\mathrm{2}} \:\mathrm{9}°\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{9}°\right)}= \\ $$$$=\frac{\mathrm{4cos}\:\mathrm{36}°}{\mathrm{sin}\:\mathrm{54}°}=\mathrm{4} \\ $$
Commented by peter frank last updated on 07/Oct/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *