Question Number 177597 by cortano1 last updated on 07/Oct/22
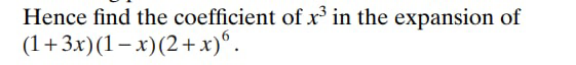
Answered by mr W last updated on 07/Oct/22
![method 1: without using formula 1×1×C_3 ^6 ×2^3 +[1×(−1)+3×1]×C_2 ^6 ×2^4 +3×(−1)×6×2^5 =64](https://www.tinkutara.com/question/Q177608.png)
$$\boldsymbol{{method}}\:\mathrm{1}:\:\boldsymbol{{without}}\:\boldsymbol{{using}}\:\boldsymbol{{formula}} \\ $$$$\mathrm{1}×\mathrm{1}×{C}_{\mathrm{3}} ^{\mathrm{6}} ×\mathrm{2}^{\mathrm{3}} \\ $$$$+\left[\mathrm{1}×\left(−\mathrm{1}\right)+\mathrm{3}×\mathrm{1}\right]×{C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{2}^{\mathrm{4}} \\ $$$$+\mathrm{3}×\left(−\mathrm{1}\right)×\mathrm{6}×\mathrm{2}^{\mathrm{5}} \\ $$$$=\mathrm{64} \\ $$
Answered by mr W last updated on 07/Oct/22

$$\boldsymbol{{method}}\:\mathrm{2}:\:\boldsymbol{{using}}\:\boldsymbol{{formula}} \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)\left(\mathrm{1}−{x}\right)\left(\mathrm{2}+{x}\right)^{\mathrm{6}} \\ $$$$=\left(\mathrm{1}+\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} \right)\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}{C}_{{k}} ^{\mathrm{6}} \mathrm{2}^{\mathrm{6}−{k}} {x}^{{k}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{3}} \:{term}: \\ $$$$\mathrm{1}×{C}_{\mathrm{3}} ^{\mathrm{6}} ×\mathrm{2}^{\mathrm{6}−\mathrm{3}} +\mathrm{2}×{C}_{\mathrm{2}} ^{\mathrm{6}} ×\mathrm{2}^{\mathrm{6}−\mathrm{2}} −\mathrm{3}×{C}_{\mathrm{1}} ^{\mathrm{6}} ×\mathrm{2}^{\mathrm{6}−\mathrm{1}} \\ $$$$=\mathrm{160}+\mathrm{480}−\mathrm{576} \\ $$$$=\mathrm{64} \\ $$
Commented by Tawa11 last updated on 09/Oct/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
