Question-177675

Question Number 177675 by cortano1 last updated on 08/Oct/22

Commented by HeferH last updated on 08/Oct/22

isn′t 10? 4x^2 + x^2 =100 x^2 = 20 A = ((20)/2) = 10 u^2

$${isn}'{t}\:\:\mathrm{10}?\: \\ $$$$\:\mathrm{4}{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} =\mathrm{100} \\ $$$$\:{x}^{\mathrm{2}} \:=\:\mathrm{20} \\ $$$$\:{A}\:=\:\frac{\mathrm{20}}{\mathrm{2}}\:=\:\mathrm{10}\:{u}^{\mathrm{2}} \\ $$

Commented by som(math1967) last updated on 08/Oct/22

$${Is}\:\mathrm{10}\:{area}?\:{or}\:{length}\:{of}\:{side}? \\ $$$$ \\ $$

Commented by HeferH last updated on 08/Oct/22

the green triangle has the same height and base,so we need (x^2 /2) (“x” would be the orange segment)

$${the}\:{green}\:{triangle}\:{has}\:{the}\:{same}\:{height}\:{and} \\ $$$$\:{base},{so}\:{we}\:{need}\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:\left(“{x}''\:{would}\:{be}\:{the}\right. \\ $$$$\left.\:{orange}\:{segment}\right) \\ $$$$\: \\ $$

Commented by cortano1 last updated on 08/Oct/22

$$\mathrm{the}\:\mathrm{request}\:\mathrm{is}\:\mathrm{green}\:\mathrm{area} \\ $$

Answered by som(math1967) last updated on 08/Oct/22

let BD=DC=x BD=DE ∴∠EBD=45⇒∠BAC=45 ∴BC=AC=2x 4x^2 +x^2 =10^2 ⇒x=2(√5) ar.of△BDE=ar. △AED [ ∵ D is mid pt ofBC ,DE∥AC ∴E is midpt ofAB] ar of △BDE=(1/2)×2(√5)×2(√5) =10sq unit A_(green) =10 sq unit [ If AD=10]

$${let}\:{BD}={DC}={x} \\ $$$${BD}={DE}\:\therefore\angle{EBD}=\mathrm{45}\Rightarrow\angle{BAC}=\mathrm{45} \\ $$$$\therefore{BC}={AC}=\mathrm{2}{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +{x}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$${ar}.{of}\bigtriangleup{BDE}={ar}.\:\bigtriangleup{AED} \\ $$$$\left[\:\because\:{D}\:{is}\:{mid}\:{pt}\:{ofBC}\:,{DE}\parallel{AC}\right. \\ $$$$\left.\therefore{E}\:{is}\:{midpt}\:{ofAB}\right] \\ $$$${ar}\:{of}\:\bigtriangleup{BDE}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{5}}×\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\:=\mathrm{10}{sq}\:{unit} \\ $$$${A}_{{green}} =\mathrm{10}\:{sq}\:{unit} \\ $$$$\left[\:{If}\:{AD}=\mathrm{10}\right] \\ $$

Commented by som(math1967) last updated on 08/Oct/22

Commented by HeferH last updated on 08/Oct/22

$${sorry}\:{if}\:{I}\:{misunderstood}\:{your}\:{question}\:{sir}, \\ $$$$\:{they}\:{have}\:{the}\:{same}\:{color}\:{so}\:{it}'{s}\:{probably} \\ $$$$\:{that}\:{way}.\: \\ $$

Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by Ar Brandon last updated on 08/Oct/22

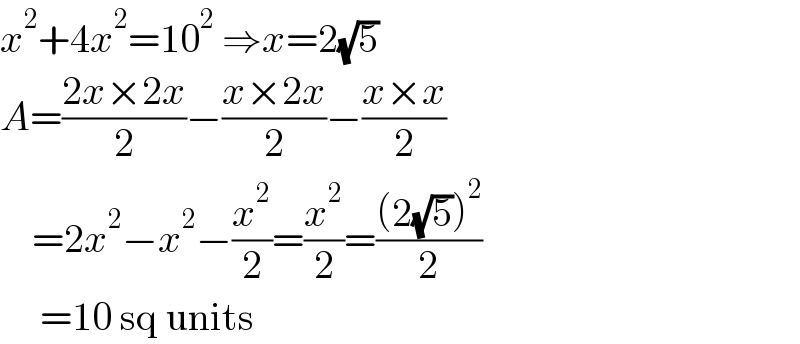
x^2 +4x^2 =10^2 ⇒x=2(√5) A=((2x×2x)/2)−((x×2x)/2)−((x×x)/2) =2x^2 −x^2 −(x^2 /2)=(x^2 /2)=(((2(√5))^2 )/2) =10 sq units

$${x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} \:\Rightarrow{x}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$${A}=\frac{\mathrm{2}{x}×\mathrm{2}{x}}{\mathrm{2}}−\frac{{x}×\mathrm{2}{x}}{\mathrm{2}}−\frac{{x}×{x}}{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\mathrm{2}}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left(\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{10}\:\mathrm{sq}\:\mathrm{units} \\ $$

Answered by a.lgnaoui last updated on 08/Oct/22

BD=DE ⇒(∡ABC=(π/4) DEB=((3π)/4) ) Posons BD=x EC=y BE=x(√(2 )) CD^2 =ED^2 +EC^2 −2ED×ECcos3(π/4) 100=x^2 +y^2 +(√2)xy (1) ((sin ∡CDE)/y)=((sin 3(π/4))/(10)) (2) ∡CDE=∡DCA ⇒sin (CDE)=sin∡ DCA=(x/(10)) ( DE ∣∣ AB) (1) ⇒(x/(10y))=((√2)/(20)) x=((y(√2))/2) (1)⇔100=(y^2 /2)+y^2 +y^2 =((5y^2 )/2) y=2(√(10)) x =2(√5) sin ∡C DE=((√5)/5) donc aire de la parrie verte Aire=10×((EH)/2)=10((xsin ∡EDC)/2)=5×2(√5) ×((√5)/5) Aire =10

$$\mathrm{BD}=\mathrm{DE}\:\Rightarrow\left(\measuredangle\mathrm{ABC}=\frac{\pi}{\mathrm{4}}\:\:\:\mathrm{DEB}=\frac{\mathrm{3}\pi}{\mathrm{4}}\:\right) \\ $$$$\mathrm{Posons}\:\mathrm{BD}={x}\:\:\:\:\mathrm{EC}={y}\:\:\:\mathrm{BE}=\mathrm{x}\sqrt{\mathrm{2}\:} \\ $$$$\mathrm{CD}^{\mathrm{2}} =\mathrm{ED}^{\mathrm{2}} +\mathrm{EC}^{\mathrm{2}} −\mathrm{2ED}×\mathrm{ECcos3}\frac{\pi}{\mathrm{4}}\: \\ $$$$\mathrm{100}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\sqrt{\mathrm{2}}{xy}\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{sin}\:\measuredangle\mathrm{CDE}}{{y}}=\frac{\mathrm{sin}\:\mathrm{3}\frac{\pi}{\mathrm{4}}}{\mathrm{10}}\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\measuredangle\mathrm{CDE}=\measuredangle\mathrm{DCA}\:\:\Rightarrow\mathrm{sin}\:\left(\mathrm{CDE}\right)=\mathrm{sin}\measuredangle\:\mathrm{DCA}=\frac{{x}}{\mathrm{10}}\:\:\:\left(\:\:\mathrm{DE}\:\:\mid\mid\:\:\mathrm{AB}\right)\: \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\Rightarrow\frac{{x}}{\mathrm{10}{y}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\:\:\:\:{x}=\frac{{y}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{100}=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+{y}^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\mathrm{5}{y}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}=\mathrm{2}\sqrt{\mathrm{10}}\:\:\:\:\:\:\:\:\:\:{x}\:=\mathrm{2}\sqrt{\mathrm{5}}\:\:\:\:\mathrm{sin}\:\measuredangle\mathrm{C}\:\mathrm{DE}=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:\:\: \\ $$$${donc}\:\:\:\:{aire}\:{de}\:{la}\:{parrie}\:{verte} \\ $$$${Aire}=\mathrm{10}×\frac{\mathrm{EH}}{\mathrm{2}}=\mathrm{10}\frac{{x}\mathrm{sin}\:\measuredangle\mathrm{EDC}}{\mathrm{2}}=\mathrm{5}×\mathrm{2}\sqrt{\mathrm{5}}\:×\frac{\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$$\:\:\boldsymbol{{A}}{ire}\:=\mathrm{10} \\ $$

Commented by a.lgnaoui last updated on 08/Oct/22

Commented by a.lgnaoui last updated on 08/Oct/22

$$\:\mathrm{H}\in\mathrm{CD}\:\:\:\mathrm{sin}\:\left(\measuredangle\mathrm{EDH}\right)=\mathrm{sin}\:\left(\measuredangle\mathrm{EDC}\right)=\frac{\mathrm{EH}}{\mathrm{ED}} \\ $$

Commented by Tawa11 last updated on 09/Oct/22

$$\mathrm{Great}\:\mathrm{sirs}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply