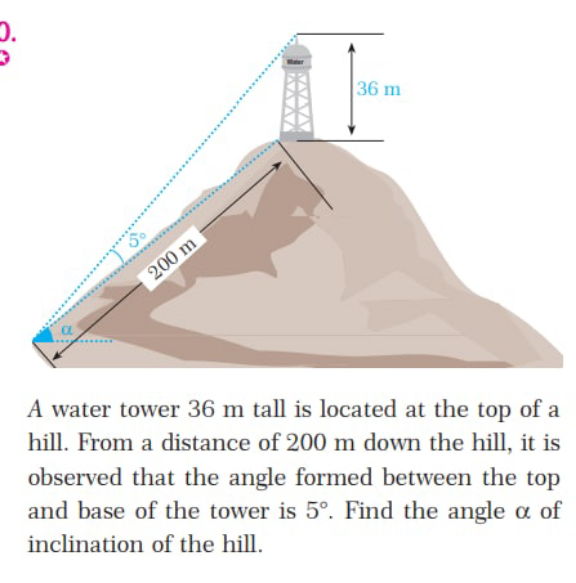
Question Number 177694 by cortano1 last updated on 08/Oct/22
Commented by Strengthenchen last updated on 08/Oct/22
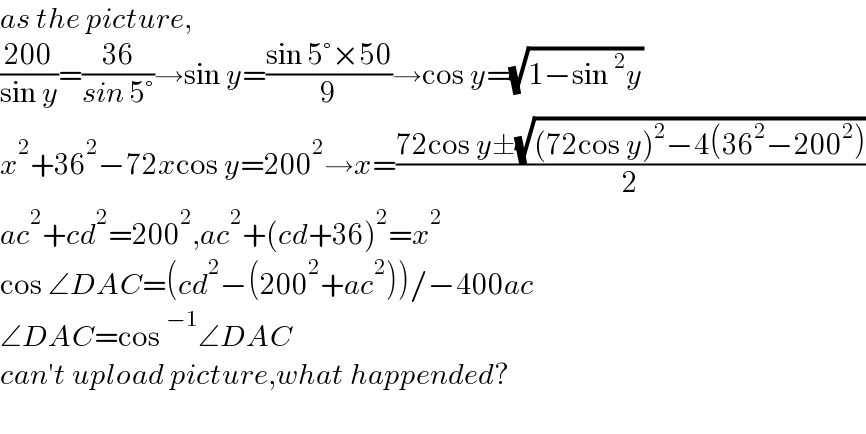
$${as}\:{the}\:{picture}, \\ $$$$\frac{\mathrm{200}}{\mathrm{sin}\:{y}}=\frac{\mathrm{36}}{{sin}\:\mathrm{5}°}\rightarrow\mathrm{sin}\:{y}=\frac{\mathrm{sin}\:\mathrm{5}°×\mathrm{50}}{\mathrm{9}}\rightarrow\mathrm{cos}\:{y}=\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {y}} \\ $$$${x}^{\mathrm{2}} +\mathrm{36}^{\mathrm{2}} −\mathrm{72}{x}\mathrm{cos}\:{y}=\mathrm{200}^{\mathrm{2}} \rightarrow{x}=\frac{\mathrm{72cos}\:{y}\pm\sqrt{\left(\mathrm{72cos}\:{y}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{36}^{\mathrm{2}} −\mathrm{200}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$${ac}^{\mathrm{2}} +{cd}^{\mathrm{2}} =\mathrm{200}^{\mathrm{2}} ,{ac}^{\mathrm{2}} +\left({cd}+\mathrm{36}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\angle{DAC}=\left({cd}^{\mathrm{2}} −\left(\mathrm{200}^{\mathrm{2}} +{ac}^{\mathrm{2}} \right)\right)/−\mathrm{400}{ac} \\ $$$$\angle{DAC}=\mathrm{cos}\:^{−\mathrm{1}} \angle{DAC} \\ $$$${can}'{t}\:{upload}\:{picture},{what}\:{happended}? \\ $$$$ \\ $$
Answered by mr W last updated on 08/Oct/22
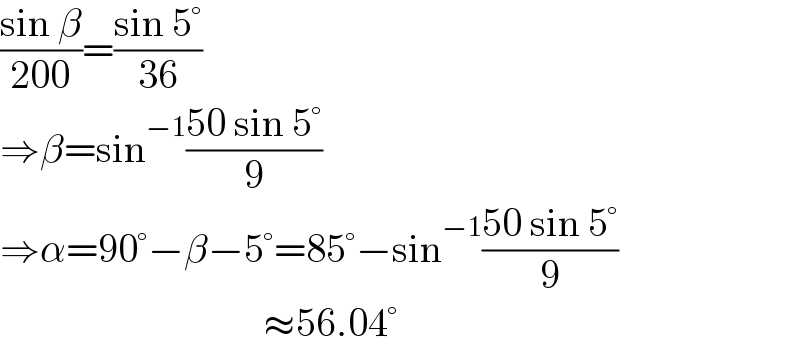
$$\frac{\mathrm{sin}\:\beta}{\mathrm{200}}=\frac{\mathrm{sin}\:\mathrm{5}°}{\mathrm{36}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{50}\:\mathrm{sin}\:\mathrm{5}°}{\mathrm{9}} \\ $$$$\Rightarrow\alpha=\mathrm{90}°−\beta−\mathrm{5}°=\mathrm{85}°−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{50}\:\mathrm{sin}\:\mathrm{5}°}{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{56}.\mathrm{04}° \\ $$
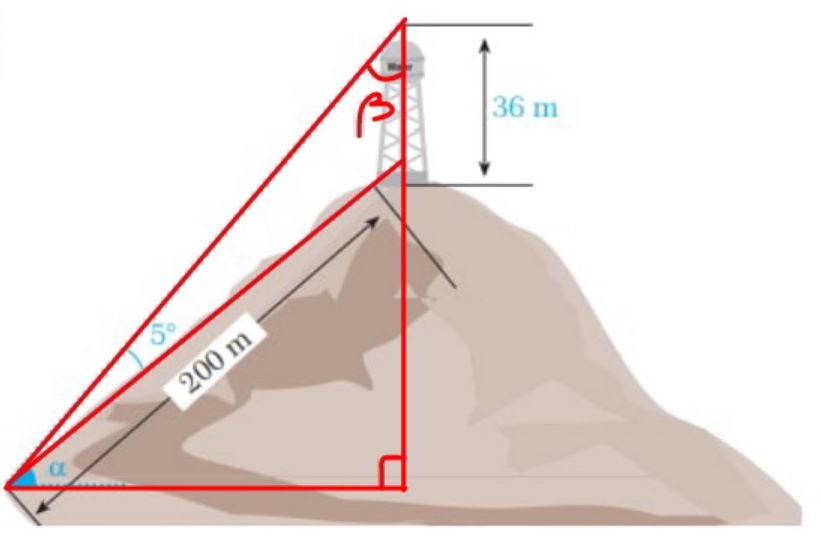
Commented by mr W last updated on 08/Oct/22
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
