Menu Close

Question-177784

Tinku Tara 0 Comments
Pin




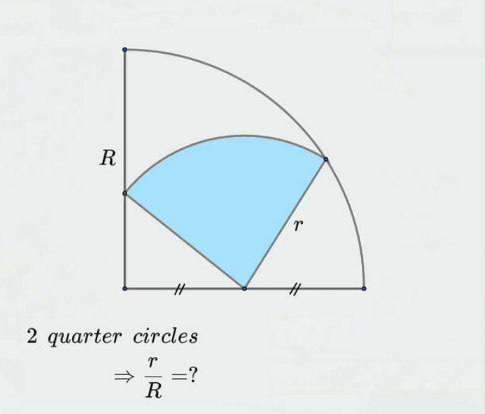
Question Number 177784 by mnjuly1970 last updated on 09/Oct/22
Answered by aleks041103 last updated on 09/Oct/22
Commented by aleks041103 last updated on 09/Oct/22
construct H∈OO′, s.t. BH⊥OO′ ΔOO′A(∡O=90°)⇒∡O′+∡A=90° ⇒α+β=90° But AOB is a quarter circle ⇒∡AO′B=90° But ∡OO′A+∡AO′B+∡BO′H=180° ⇒α+∡BO′H=90° ⇒∡BO′H=β But by construction for ΔHO′B(∡H=90°) ⇒∡HO′B+∡O′BH=90° ⇒∡O′BH=α ⇒ΔO′OA=ΔBHO′ since: 1. both are right Δ 2. ∡O′BH=∡OO′A 3. AO′=O′B=r ⇒BH=OO′=(R/2) ∡OHB=90° and OB=R ⇒OH=(√(R^2 −((R/2))^2 ))=((√3)/2)R ⇒O′H=OH−OO′=(((√3)−1)/2)R ⇒O′B=(√(((((√3)−1)/2)R)^2 +((R/2))^2 ))= =(R/2)(√(((√3)−1)^2 +1))=((√(5−2(√3)))/2)R=r ⇒(r/R)=((√(5−2(√3)))/2)
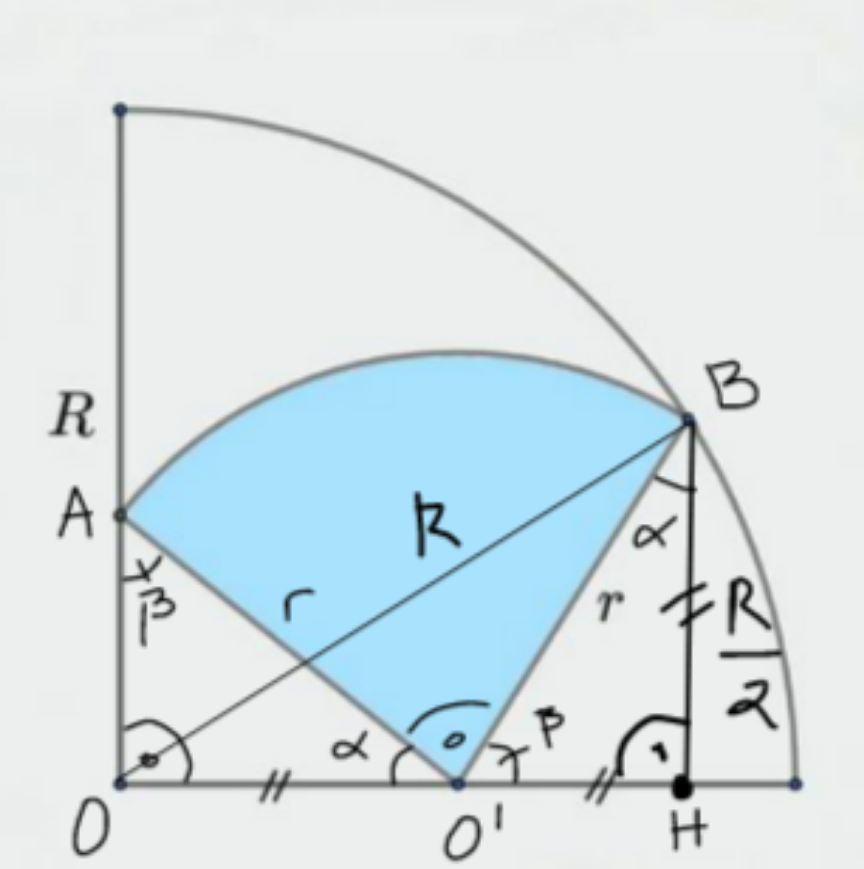
$${construct} \\ $$$${H}\in{OO}',\:{s}.{t}.\:{BH}\bot{OO}' \\ $$$$\Delta{OO}'{A}\left(\measuredangle{O}=\mathrm{90}°\right)\Rightarrow\measuredangle{O}'+\measuredangle{A}=\mathrm{90}° \\ $$$$\Rightarrow\alpha+\beta=\mathrm{90}° \\ $$$${But}\:{AOB}\:{is}\:{a}\:{quarter}\:{circle} \\ $$$$\Rightarrow\measuredangle{AO}'{B}=\mathrm{90}° \\ $$$${But} \\ $$$$\measuredangle{OO}'{A}+\measuredangle{AO}'{B}+\measuredangle{BO}'{H}=\mathrm{180}° \\ $$$$\Rightarrow\alpha+\measuredangle{BO}'{H}=\mathrm{90}° \\ $$$$\Rightarrow\measuredangle{BO}'{H}=\beta \\ $$$${But}\:{by}\:{construction}\:{for}\:\Delta{HO}'{B}\left(\measuredangle{H}=\mathrm{90}°\right) \\ $$$$\Rightarrow\measuredangle{HO}'{B}+\measuredangle{O}'{BH}=\mathrm{90}° \\ $$$$\Rightarrow\measuredangle{O}'{BH}=\alpha \\ $$$$\Rightarrow\Delta{O}'{OA}=\Delta{BHO}' \\ $$$${since}: \\ $$$$\mathrm{1}.\:{both}\:{are}\:{right}\:\Delta \\ $$$$\mathrm{2}.\:\measuredangle{O}'{BH}=\measuredangle{OO}'{A} \\ $$$$\mathrm{3}.\:{AO}'={O}'{B}={r} \\ $$$$\Rightarrow{BH}={OO}'=\frac{{R}}{\mathrm{2}} \\ $$$$\measuredangle{OHB}=\mathrm{90}°\:{and}\:{OB}={R} \\ $$$$\Rightarrow{OH}=\sqrt{{R}^{\mathrm{2}} −\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{R} \\ $$$$\Rightarrow{O}'{H}={OH}−{OO}'=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}{R} \\ $$$$\Rightarrow{O}'{B}=\sqrt{\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}{R}\right)^{\mathrm{2}} +\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{R}}{\mathrm{2}}\sqrt{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}}{R}={r} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 09/Oct/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *