Question Number 177815 by infinityaction last updated on 09/Oct/22
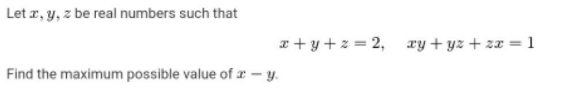
Answered by mahdipoor last updated on 09/Oct/22
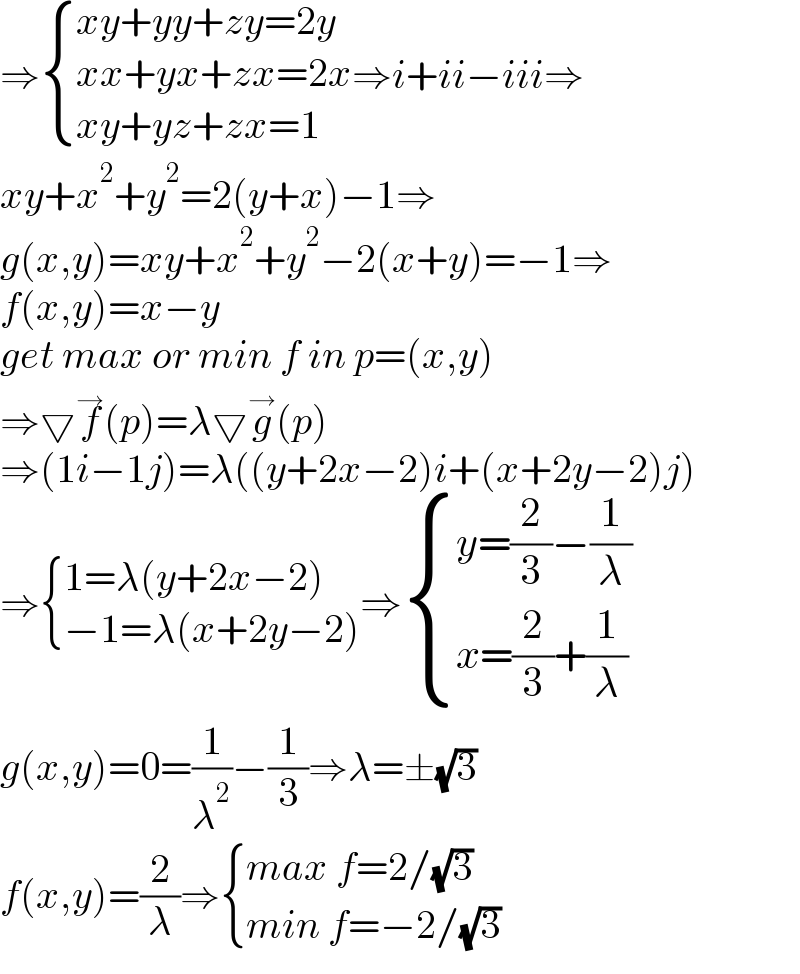
$$\Rightarrow\begin{cases}{{xy}+{yy}+{zy}=\mathrm{2}{y}}\\{{xx}+{yx}+{zx}=\mathrm{2}{x}}\\{{xy}+{yz}+{zx}=\mathrm{1}}\end{cases}\Rightarrow{i}+{ii}−{iii}\Rightarrow \\ $$$${xy}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}\left({y}+{x}\right)−\mathrm{1}\Rightarrow \\ $$$${g}\left({x},{y}\right)={xy}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}\left({x}+{y}\right)=−\mathrm{1}\Rightarrow \\ $$$${f}\left({x},{y}\right)={x}−{y} \\ $$$${get}\:{max}\:{or}\:{min}\:{f}\:{in}\:{p}=\left({x},{y}\right) \\ $$$$\Rightarrow\bigtriangledown\overset{\rightarrow} {{f}}\left({p}\right)=\lambda\bigtriangledown\overset{\rightarrow} {{g}}\left({p}\right) \\ $$$$\Rightarrow\left(\mathrm{1}{i}−\mathrm{1}{j}\right)=\lambda\left(\left({y}+\mathrm{2}{x}−\mathrm{2}\right){i}+\left({x}+\mathrm{2}{y}−\mathrm{2}\right){j}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{1}=\lambda\left({y}+\mathrm{2}{x}−\mathrm{2}\right)}\\{−\mathrm{1}=\lambda\left({x}+\mathrm{2}{y}−\mathrm{2}\right)}\end{cases}\Rightarrow\begin{cases}{{y}=\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\lambda}}\\{{x}=\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\lambda}}\end{cases} \\ $$$${g}\left({x},{y}\right)=\mathrm{0}=\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\lambda=\pm\sqrt{\mathrm{3}} \\ $$$${f}\left({x},{y}\right)=\frac{\mathrm{2}}{\lambda}\Rightarrow\begin{cases}{{max}\:{f}=\mathrm{2}/\sqrt{\mathrm{3}}}\\{{min}\:{f}=−\mathrm{2}/\sqrt{\mathrm{3}}}\end{cases} \\ $$
Commented by infinityaction last updated on 09/Oct/22

$${thanks}\:{sir} \\ $$
Commented by Tawa11 last updated on 10/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 09/Oct/22
![x+y=2−z xy+(x+y)z=1 xy=1−z(2−z) (x−y)^2 =(x+y)^2 −4xy =(2−z)^2 −4[1−z(2−z)] =4z−3z^2 =−3(z−(2/3))^2 +(4/3)≤(4/3) ⇒∣x−y∣≤(2/( (√3))) ⇒−(2/( (√3)))≤x−y≤(2/( (√3))) ⇒(x−y)_(max) =(2/( (√3))) at z=(2/3) ⇒(x−y)_(min) =−(2/( (√3))) at z=(2/3)](https://www.tinkutara.com/question/Q177831.png)
$${x}+{y}=\mathrm{2}−{z} \\ $$$${xy}+\left({x}+{y}\right){z}=\mathrm{1} \\ $$$${xy}=\mathrm{1}−{z}\left(\mathrm{2}−{z}\right) \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy} \\ $$$$\:\:=\left(\mathrm{2}−{z}\right)^{\mathrm{2}} −\mathrm{4}\left[\mathrm{1}−{z}\left(\mathrm{2}−{z}\right)\right] \\ $$$$\:\:=\mathrm{4}{z}−\mathrm{3}{z}^{\mathrm{2}} \\ $$$$\:\:=−\mathrm{3}\left({z}−\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{3}}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\mid{x}−{y}\mid\leqslant\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\leqslant{x}−{y}\leqslant\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\left({x}−{y}\right)_{{max}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{at}\:{z}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\left({x}−{y}\right)_{{min}} =−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{at}\:{z}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by infinityaction last updated on 09/Oct/22

$${thank}\:{you}\:{sir} \\ $$
Commented by Tawa11 last updated on 10/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
