Question Number 177835 by infinityaction last updated on 09/Oct/22
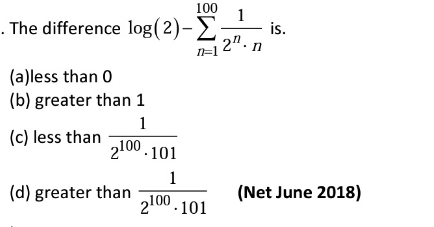
Answered by mr W last updated on 09/Oct/22
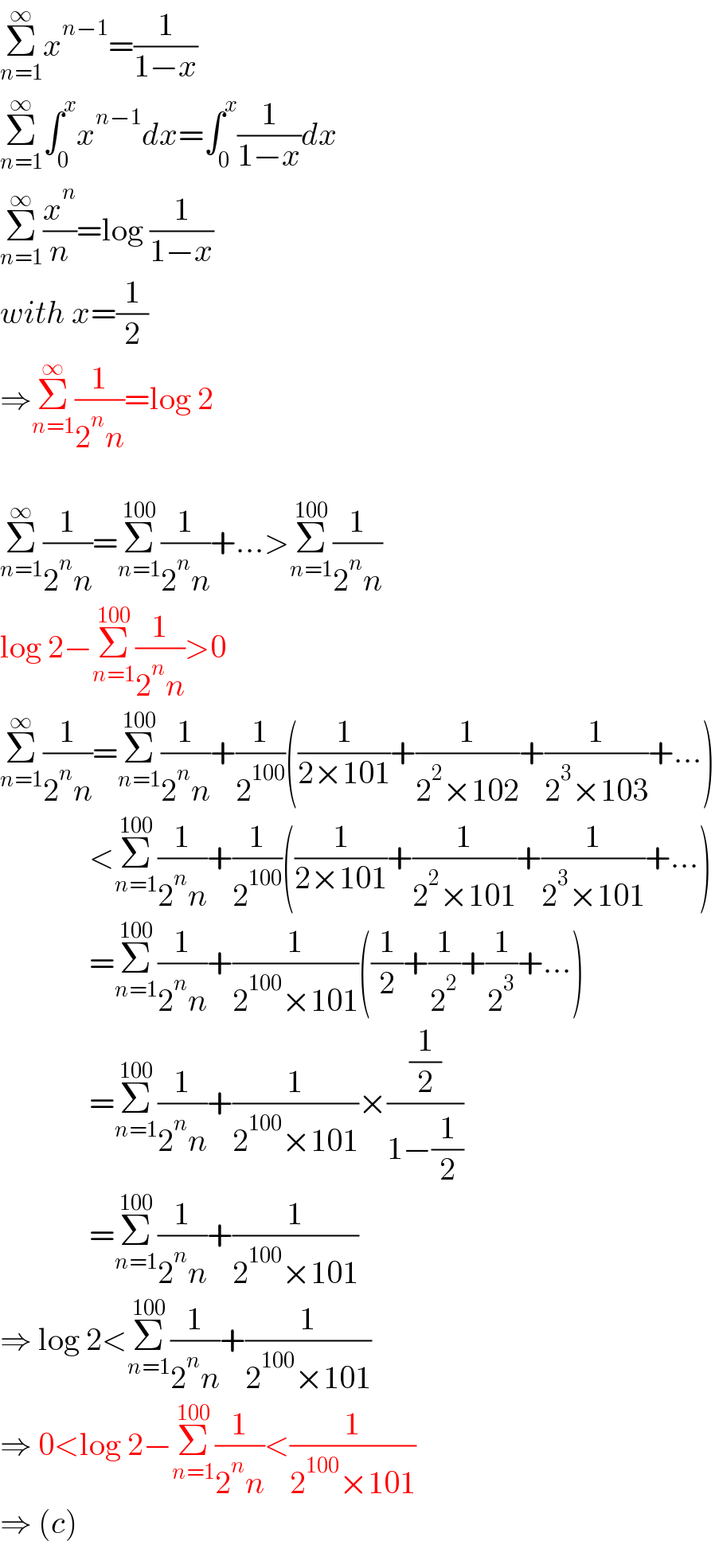
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} {x}^{{n}−\mathrm{1}} {dx}=\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}=\mathrm{log}\:\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${with}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}=\mathrm{log}\:\mathrm{2} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+…>\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}} \\ $$$$\mathrm{log}\:\mathrm{2}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}>\mathrm{0} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} }\left(\frac{\mathrm{1}}{\mathrm{2}×\mathrm{101}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} ×\mathrm{102}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} ×\mathrm{103}}+…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:<\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} }\left(\frac{\mathrm{1}}{\mathrm{2}×\mathrm{101}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} ×\mathrm{101}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} ×\mathrm{101}}+…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} ×\mathrm{101}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} ×\mathrm{101}}×\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} ×\mathrm{101}} \\ $$$$\Rightarrow\:\mathrm{log}\:\mathrm{2}<\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} ×\mathrm{101}} \\ $$$$\Rightarrow\:\mathrm{0}<\mathrm{log}\:\mathrm{2}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}}<\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{100}} ×\mathrm{101}}\:\: \\ $$$$\Rightarrow\:\left({c}\right) \\ $$
Commented by Tawa11 last updated on 10/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by infinityaction last updated on 10/Oct/22

$${thanks}\:{sir}\: \\ $$
