Question Number 177848 by mathdave last updated on 09/Oct/22

Commented by mathdave last updated on 09/Oct/22
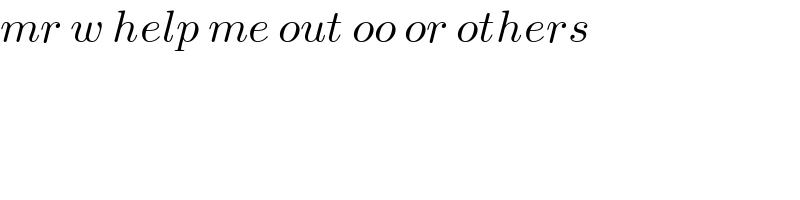
$${mr}\:{w}\:{help}\:{me}\:{out}\:{oo}\:{or}\:{others} \\ $$
Commented by mr W last updated on 10/Oct/22
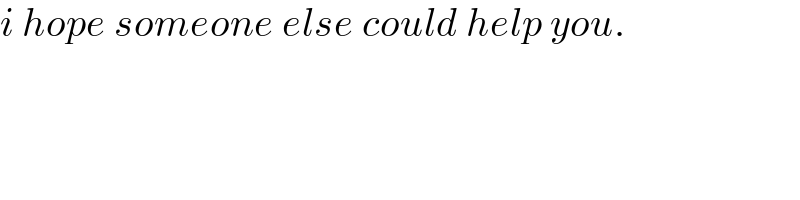
$${i}\:{hope}\:{someone}\:{else}\:{could}\:{help}\:{you}. \\ $$
Commented by York12 last updated on 22/May/23

$${you}\:{are}\:{uploading}\:{your}\:{assigments}\:{on}\:{the} \\ $$$${forum}\: \\ $$$${and}\:{harrying}\:{us}\:{up}\:{to}\:{solve}\:{them}\: \\ $$$${you}\:{are}\:{stupid}\:{or}\:{simply}\:{lazy} \\ $$
Answered by Spillover last updated on 10/Oct/22
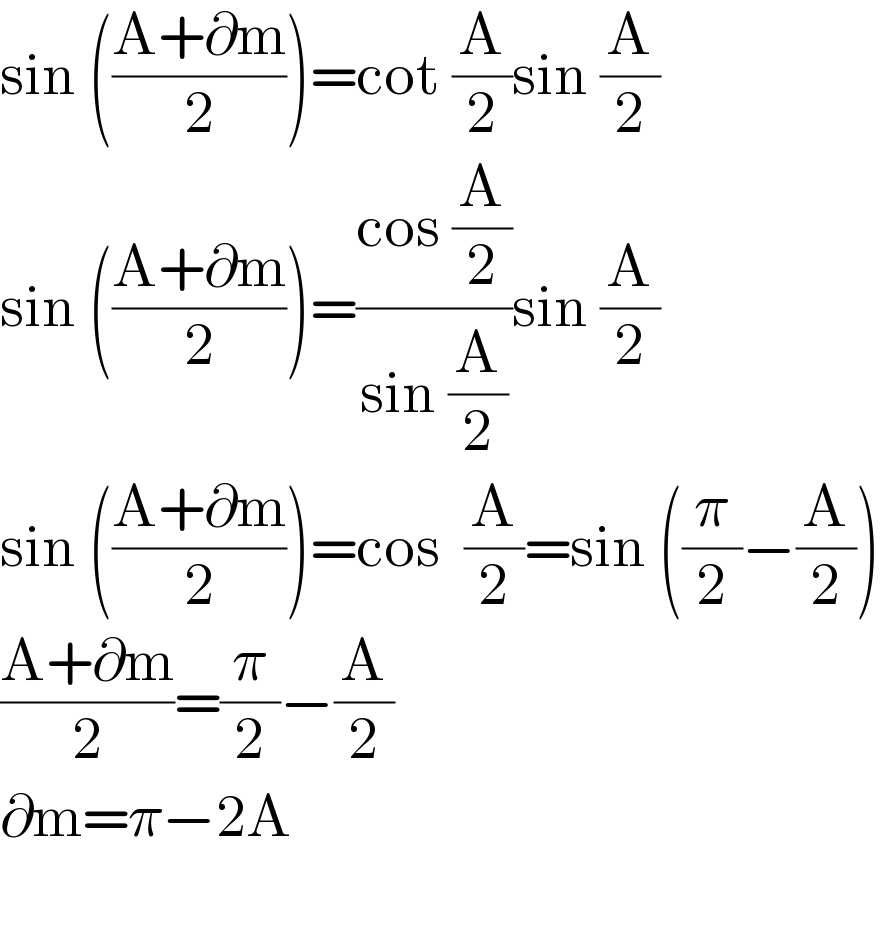
$$\mathrm{sin}\:\left(\frac{\mathrm{A}+\partial\mathrm{m}}{\mathrm{2}}\right)=\mathrm{cot}\:\frac{\mathrm{A}}{\mathrm{2}}\mathrm{sin}\:\frac{\mathrm{A}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{A}+\partial\mathrm{m}}{\mathrm{2}}\right)=\frac{\mathrm{cos}\:\frac{\mathrm{A}}{\mathrm{2}}}{\mathrm{sin}\:\frac{\mathrm{A}}{\mathrm{2}}}\mathrm{sin}\:\frac{\mathrm{A}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{A}+\partial\mathrm{m}}{\mathrm{2}}\right)=\mathrm{cos}\:\:\frac{\mathrm{A}}{\mathrm{2}}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{A}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{A}+\partial\mathrm{m}}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{A}}{\mathrm{2}} \\ $$$$\partial\mathrm{m}=\pi−\mathrm{2A} \\ $$$$ \\ $$
Commented by mathdave last updated on 10/Oct/22
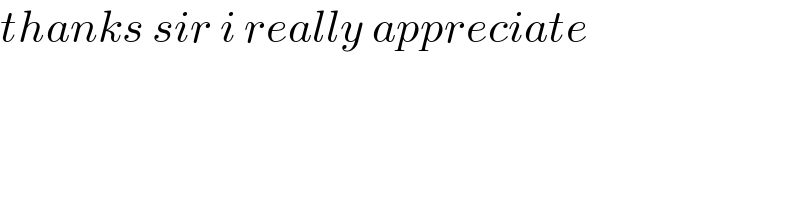
$${thanks}\:{sir}\:{i}\:{really}\:{appreciate} \\ $$
Answered by Spillover last updated on 10/Oct/22
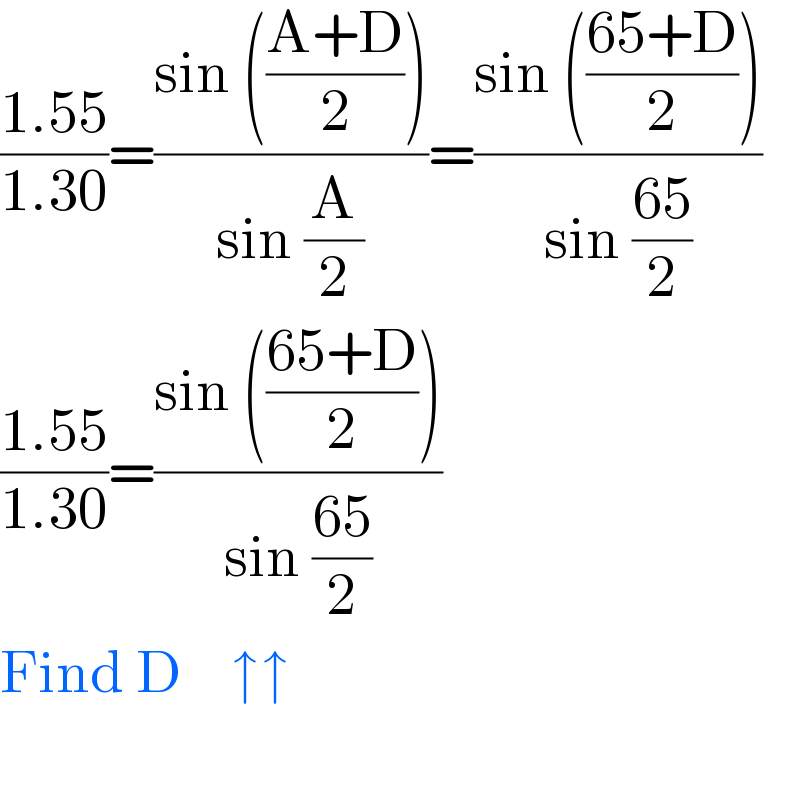
$$\frac{\mathrm{1}.\mathrm{55}}{\mathrm{1}.\mathrm{30}}=\frac{\mathrm{sin}\:\left(\frac{\mathrm{A}+\mathrm{D}}{\mathrm{2}}\right)}{\mathrm{sin}\:\frac{\mathrm{A}}{\mathrm{2}}}=\frac{\mathrm{sin}\:\left(\frac{\mathrm{65}+\mathrm{D}}{\mathrm{2}}\right)}{\mathrm{sin}\:\frac{\mathrm{65}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}.\mathrm{55}}{\mathrm{1}.\mathrm{30}}=\frac{\mathrm{sin}\:\left(\frac{\mathrm{65}+\mathrm{D}}{\mathrm{2}}\right)}{\mathrm{sin}\:\frac{\mathrm{65}}{\mathrm{2}}} \\ $$$$\mathrm{Find}\:\mathrm{D}\:\:\:\:\uparrow\uparrow \\ $$$$ \\ $$
