Question Number 177880 by DAVONG last updated on 10/Oct/22

Answered by mr W last updated on 10/Oct/22
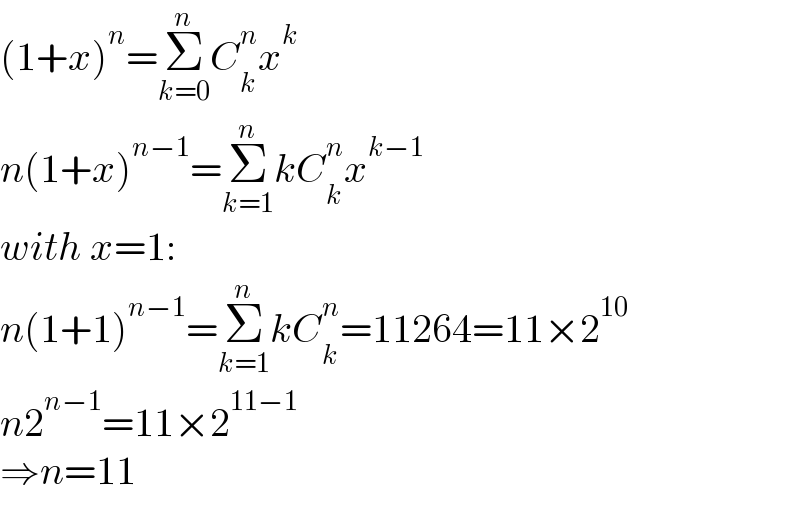
$$\left(\mathrm{1}+{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{{n}} {x}^{{k}} \\ $$$${n}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{kC}_{{k}} ^{{n}} {x}^{{k}−\mathrm{1}} \\ $$$${with}\:{x}=\mathrm{1}: \\ $$$${n}\left(\mathrm{1}+\mathrm{1}\right)^{{n}−\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{kC}_{{k}} ^{{n}} =\mathrm{11264}=\mathrm{11}×\mathrm{2}^{\mathrm{10}} \\ $$$${n}\mathrm{2}^{{n}−\mathrm{1}} =\mathrm{11}×\mathrm{2}^{\mathrm{11}−\mathrm{1}} \\ $$$$\Rightarrow{n}=\mathrm{11} \\ $$
Commented by DAVONG last updated on 10/Oct/22

$$\mathrm{Thanks}\:\mathrm{teacher} \\ $$
Commented by Tawa11 last updated on 10/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
