Menu Close

Question-177910

Tinku Tara 0 Comments
Pin




Question Number 177910 by HeferH last updated on 11/Oct/22
Answered by mr W last updated on 11/Oct/22
Commented by mr W last updated on 11/Oct/22
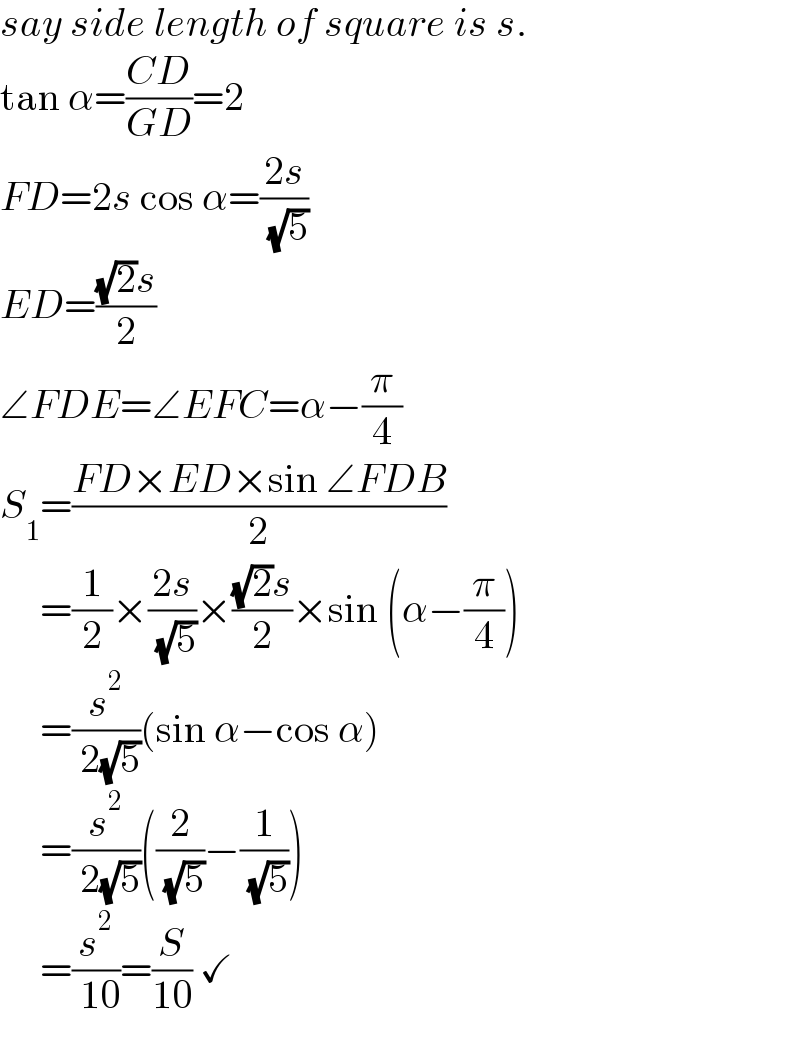
say side length of square is s. tan α=((CD)/(GD))=2 FD=2s cos α=((2s)/( (√5))) ED=(((√2)s)/2) ∠FDE=∠EFC=α−(π/4) S_1 =((FD×ED×sin ∠FDB)/2) =(1/2)×((2s)/( (√5)))×(((√2)s)/2)×sin (α−(π/4)) =(s^2 /( 2(√5)))(sin α−cos α) =(s^2 /( 2(√5)))((2/( (√5)))−(1/( (√5)))) =(s^2 /( 10))=(S/(10)) ✓
$${say}\:{side}\:{length}\:{of}\:{square}\:{is}\:{s}. \\ $$$$\mathrm{tan}\:\alpha=\frac{{CD}}{{GD}}=\mathrm{2} \\ $$$${FD}=\mathrm{2}{s}\:\mathrm{cos}\:\alpha=\frac{\mathrm{2}{s}}{\:\sqrt{\mathrm{5}}} \\ $$$${ED}=\frac{\sqrt{\mathrm{2}}{s}}{\mathrm{2}} \\ $$$$\angle{FDE}=\angle{EFC}=\alpha−\frac{\pi}{\mathrm{4}} \\ $$$${S}_{\mathrm{1}} =\frac{{FD}×{ED}×\mathrm{sin}\:\angle{FDB}}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{s}}{\:\sqrt{\mathrm{5}}}×\frac{\sqrt{\mathrm{2}}{s}}{\mathrm{2}}×\mathrm{sin}\:\left(\alpha−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:=\frac{{s}^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\mathrm{5}}}\left(\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha\right) \\ $$$$\:\:\:\:\:=\frac{{s}^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\mathrm{5}}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\:\:\:\:\:=\frac{{s}^{\mathrm{2}} }{\:\mathrm{10}}=\frac{{S}}{\mathrm{10}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 11/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by kapoorshah last updated on 11/Oct/22
Commented by kapoorshah last updated on 11/Oct/22
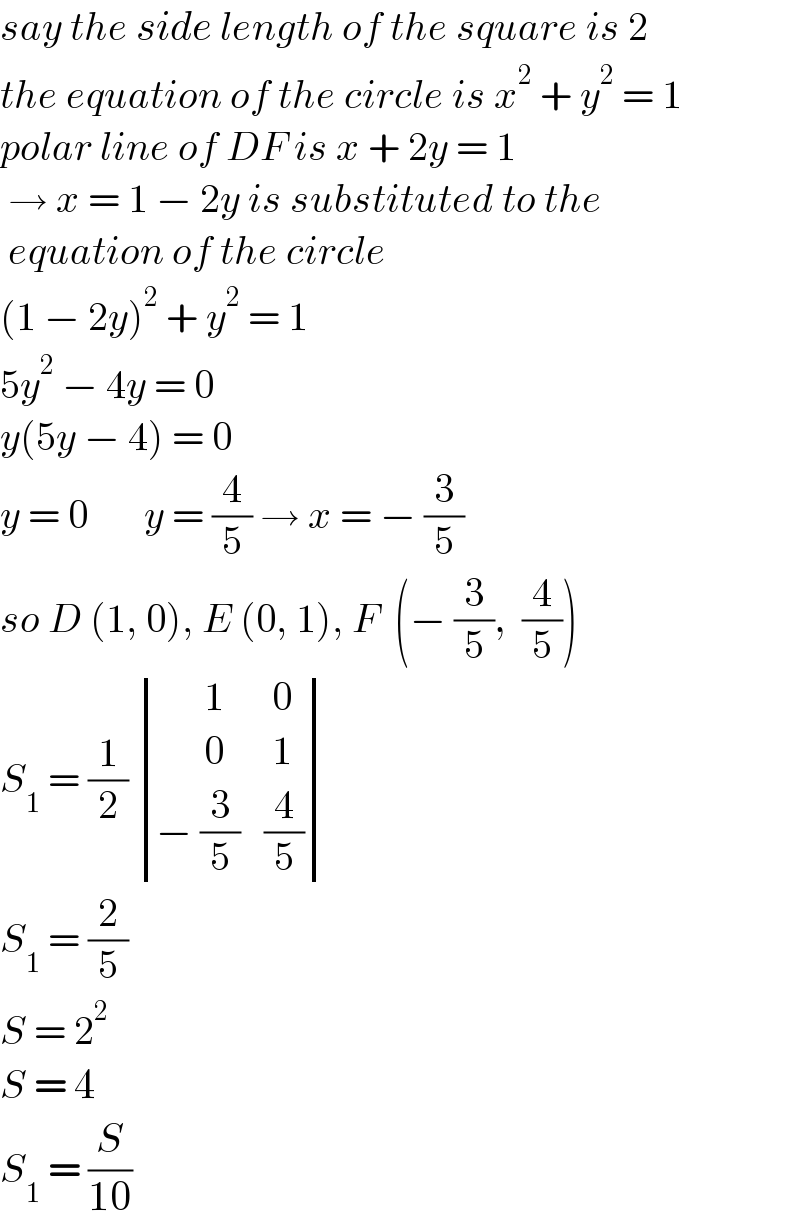
say the side length of the square is 2 the equation of the circle is x^2 + y^2 = 1 polar line of DF is x + 2y = 1 → x = 1 − 2y is substituted to the equation of the circle (1 − 2y)^2 + y^2 = 1 5y^2 − 4y = 0 y(5y − 4) = 0 y = 0 y = (4/5) → x = − (3/5) so D (1, 0), E (0, 1), F (− (3/5), (4/5)) S_1 = (1/2) determinant ((( 1),( 0)),(( 0),( 1)),((− (3/5)),(4/5))) S_1 = (2/5) S = 2^2 S = 4 S_1 = (S/(10))
$${say}\:{the}\:{side}\:{length}\:{of}\:{the}\:{square}\:{is}\:\mathrm{2} \\ $$$${the}\:{equation}\:{of}\:{the}\:{circle}\:{is}\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$${polar}\:{line}\:{of}\:{DF}\:{is}\:{x}\:+\:\mathrm{2}{y}\:=\:\mathrm{1} \\ $$$$\:\rightarrow\:{x}\:=\:\mathrm{1}\:−\:\mathrm{2}{y}\:{is}\:{substituted}\:{to}\:{the} \\ $$$$\:{equation}\:{of}\:{the}\:{circle} \\ $$$$\left(\mathrm{1}\:−\:\mathrm{2}{y}\right)^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\mathrm{5}{y}^{\mathrm{2}} \:−\:\mathrm{4}{y}\:=\:\mathrm{0} \\ $$$${y}\left(\mathrm{5}{y}\:−\:\mathrm{4}\right)\:=\:\mathrm{0} \\ $$$${y}\:=\:\mathrm{0}\:\:\:\:\:\:\:{y}\:=\:\frac{\mathrm{4}}{\mathrm{5}}\:\rightarrow\:{x}\:=\:−\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${so}\:{D}\:\left(\mathrm{1},\:\mathrm{0}\right),\:{E}\:\left(\mathrm{0},\:\mathrm{1}\right),\:{F}\:\:\left(−\:\frac{\mathrm{3}}{\mathrm{5}},\:\:\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$${S}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\begin{vmatrix}{\:\:\:\:\:\:\mathrm{1}}&{\:\mathrm{0}}\\{\:\:\:\:\:\:\mathrm{0}}&{\:\mathrm{1}}\\{−\:\frac{\mathrm{3}}{\mathrm{5}}}&{\frac{\mathrm{4}}{\mathrm{5}}}\end{vmatrix} \\ $$$${S}_{\mathrm{1}} \:=\:\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${S}\:=\:\mathrm{2}^{\mathrm{2}} \\ $$$${S}\:=\:\mathrm{4} \\ $$$${S}_{\mathrm{1}} \:=\:\frac{{S}}{\mathrm{10}} \\ $$
Commented by Tawa11 last updated on 11/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *