Question-177922

Question Number 177922 by Lekhraj last updated on 11/Oct/22

Answered by mr W last updated on 11/Oct/22

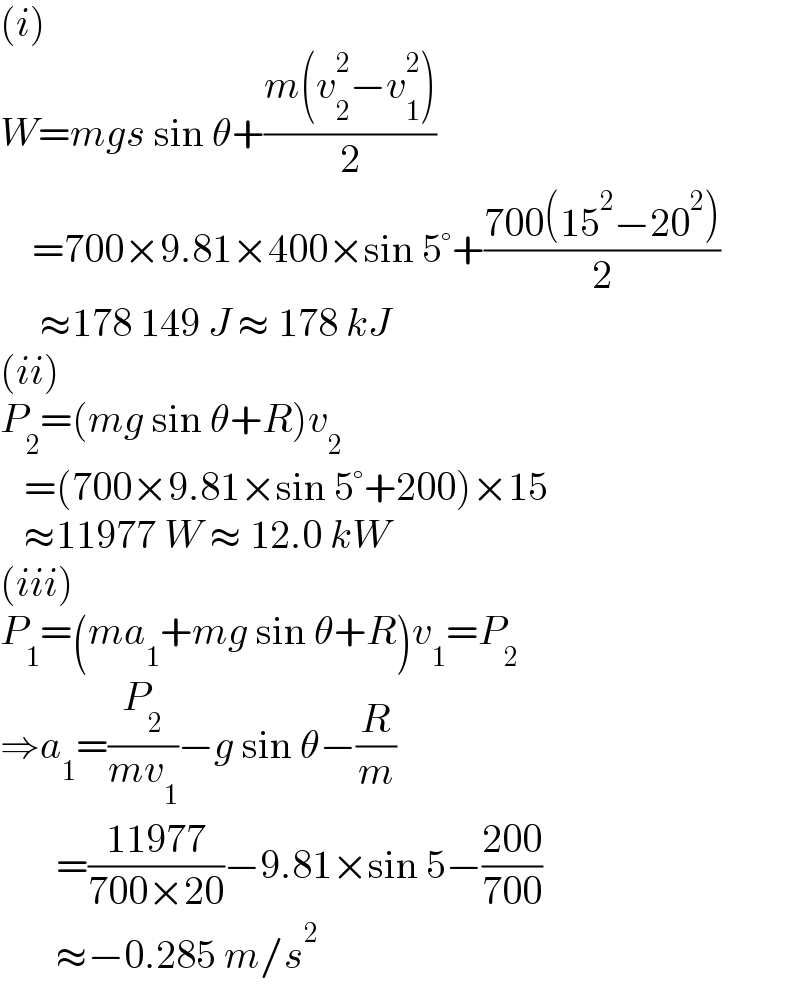
(i) W=mgs sin θ+((m(v_2 ^2 −v_1 ^2 ))/2) =700×9.81×400×sin 5°+((700(15^2 −20^2 ))/2) ≈178 149 J ≈ 178 kJ (ii) P_2 =(mg sin θ+R)v_2 =(700×9.81×sin 5°+200)×15 ≈11977 W ≈ 12.0 kW (iii) P_1 =(ma_1 +mg sin θ+R)v_1 =P_2 ⇒a_1 =(P_2 /(mv_1 ))−g sin θ−(R/m) =((11977)/(700×20))−9.81×sin 5−((200)/(700)) ≈−0.285 m/s^2

$$\left({i}\right) \\ $$$${W}={mgs}\:\mathrm{sin}\:\theta+\frac{{m}\left({v}_{\mathrm{2}} ^{\mathrm{2}} −{v}_{\mathrm{1}} ^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{700}×\mathrm{9}.\mathrm{81}×\mathrm{400}×\mathrm{sin}\:\mathrm{5}°+\frac{\mathrm{700}\left(\mathrm{15}^{\mathrm{2}} −\mathrm{20}^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\approx\mathrm{178}\:\mathrm{149}\:{J}\:\approx\:\mathrm{178}\:{kJ} \\ $$$$\left({ii}\right) \\ $$$${P}_{\mathrm{2}} =\left({mg}\:\mathrm{sin}\:\theta+{R}\right){v}_{\mathrm{2}} \\ $$$$\:\:\:=\left(\mathrm{700}×\mathrm{9}.\mathrm{81}×\mathrm{sin}\:\mathrm{5}°+\mathrm{200}\right)×\mathrm{15} \\ $$$$\:\:\:\approx\mathrm{11977}\:{W}\:\approx\:\mathrm{12}.\mathrm{0}\:{kW} \\ $$$$\left({iii}\right) \\ $$$${P}_{\mathrm{1}} =\left({ma}_{\mathrm{1}} +{mg}\:\mathrm{sin}\:\theta+{R}\right){v}_{\mathrm{1}} ={P}_{\mathrm{2}} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\frac{{P}_{\mathrm{2}} }{{mv}_{\mathrm{1}} }−{g}\:\mathrm{sin}\:\theta−\frac{{R}}{{m}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{11977}}{\mathrm{700}×\mathrm{20}}−\mathrm{9}.\mathrm{81}×\mathrm{sin}\:\mathrm{5}−\frac{\mathrm{200}}{\mathrm{700}} \\ $$$$\:\:\:\:\:\:\:\approx−\mathrm{0}.\mathrm{285}\:{m}/{s}^{\mathrm{2}} \\ $$

Commented by Lekhraj last updated on 11/Oct/22

$${thank}\:{you}\: \\ $$

Commented by Tawa11 last updated on 11/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply