Menu Close

Question-177978

Tinku Tara 0 Comments
Pin




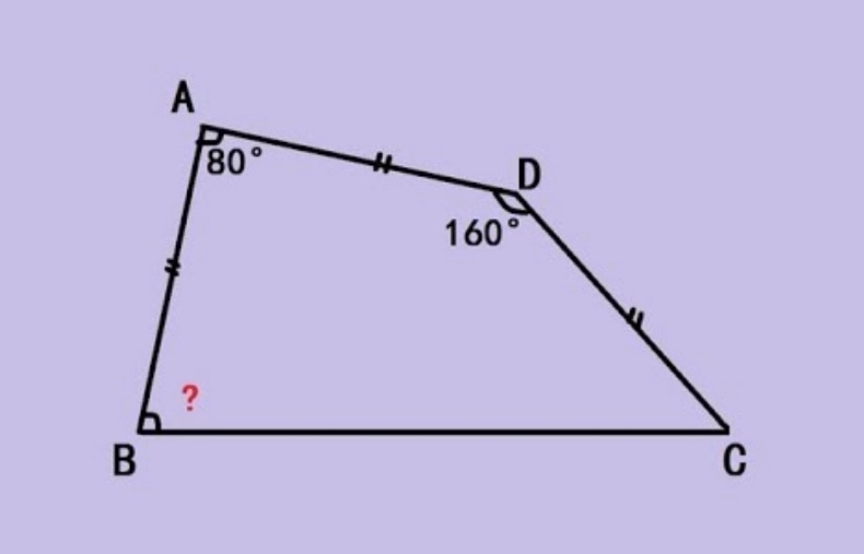
Question Number 177978 by mr W last updated on 11/Oct/22
Answered by mr W last updated on 11/Oct/22
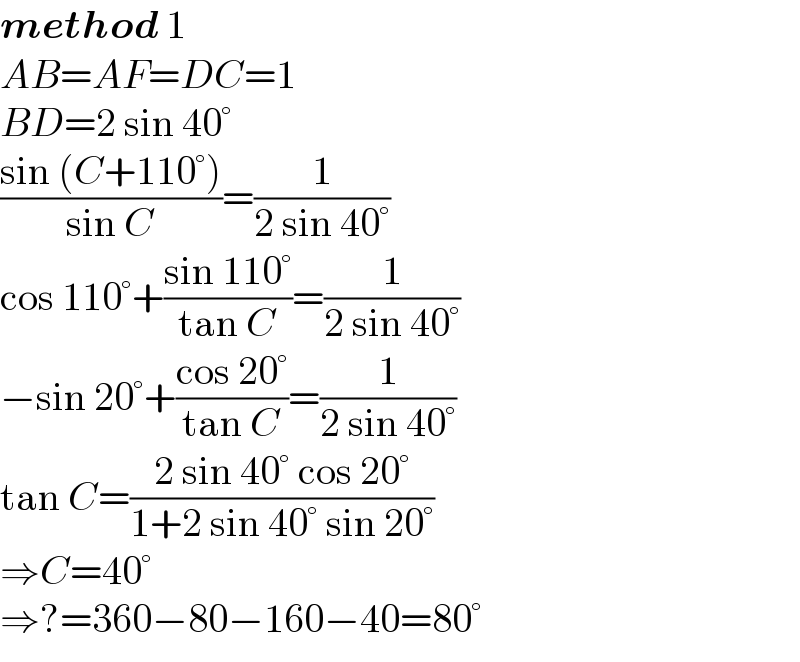
method 1 AB=AF=DC=1 BD=2 sin 40° ((sin (C+110°))/(sin C))=(1/(2 sin 40°)) cos 110°+((sin 110°)/(tan C))=(1/(2 sin 40°)) −sin 20°+((cos 20°)/(tan C))=(1/(2 sin 40°)) tan C=((2 sin 40° cos 20°)/(1+2 sin 40° sin 20°)) ⇒C=40° ⇒?=360−80−160−40=80°
$$\boldsymbol{{method}}\:\mathrm{1} \\ $$$${AB}={AF}={DC}=\mathrm{1} \\ $$$${BD}=\mathrm{2}\:\mathrm{sin}\:\mathrm{40}° \\ $$$$\frac{\mathrm{sin}\:\left({C}+\mathrm{110}°\right)}{\mathrm{sin}\:{C}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{40}°} \\ $$$$\mathrm{cos}\:\mathrm{110}°+\frac{\mathrm{sin}\:\mathrm{110}°}{\mathrm{tan}\:{C}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{40}°} \\ $$$$−\mathrm{sin}\:\mathrm{20}°+\frac{\mathrm{cos}\:\mathrm{20}°}{\mathrm{tan}\:{C}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{40}°} \\ $$$$\mathrm{tan}\:{C}=\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{40}°\:\mathrm{cos}\:\mathrm{20}°}{\mathrm{1}+\mathrm{2}\:\mathrm{sin}\:\mathrm{40}°\:\mathrm{sin}\:\mathrm{20}°} \\ $$$$\Rightarrow{C}=\mathrm{40}° \\ $$$$\Rightarrow?=\mathrm{360}−\mathrm{80}−\mathrm{160}−\mathrm{40}=\mathrm{80}° \\ $$
Commented by Tawa11 last updated on 11/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 11/Oct/22
Commented by mr W last updated on 11/Oct/22
method 2 let AE//DC, CE//CD ⇒ADCE is parallelogram ⇒AE=AD=AB ∠BAE=80−20=60° ⇒ΔABE is equilateral ⇒BE=AE=AD=EC ⇒ΔBEC is isosceles ⇒∠EBC=((180−140)/2)=20° ⇒?=60+20=80° ✓
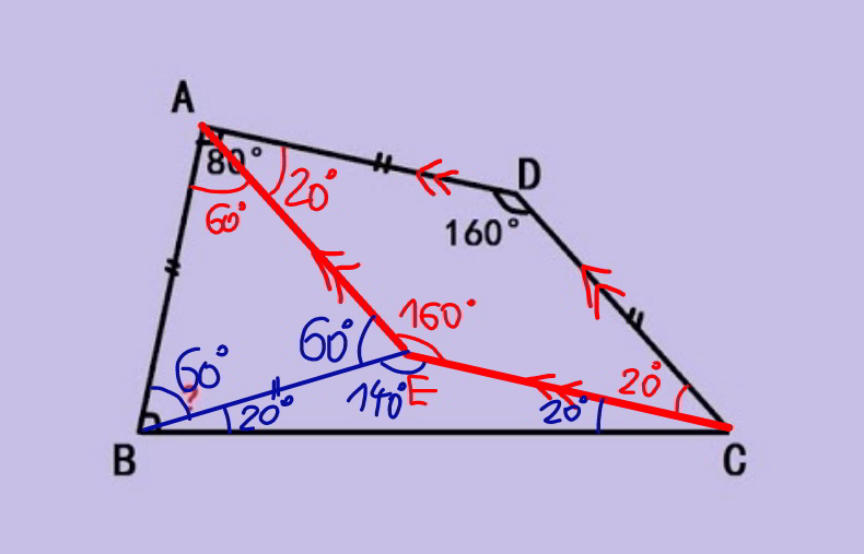
$$\boldsymbol{{method}}\:\mathrm{2} \\ $$$${let}\:{AE}//{DC},\:{CE}//{CD} \\ $$$$\Rightarrow{ADCE}\:{is}\:{parallelogram} \\ $$$$\Rightarrow{AE}={AD}={AB} \\ $$$$\angle{BAE}=\mathrm{80}−\mathrm{20}=\mathrm{60}° \\ $$$$\Rightarrow\Delta{ABE}\:{is}\:{equilateral} \\ $$$$\Rightarrow{BE}={AE}={AD}={EC} \\ $$$$\Rightarrow\Delta{BEC}\:{is}\:{isosceles} \\ $$$$\Rightarrow\angle{EBC}=\frac{\mathrm{180}−\mathrm{140}}{\mathrm{2}}=\mathrm{20}° \\ $$$$\Rightarrow?=\mathrm{60}+\mathrm{20}=\mathrm{80}°\:\checkmark \\ $$
Commented by Tawa11 last updated on 11/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by a.lgnaoui last updated on 11/Oct/22
ΔADC AD=DC ⇒∡DAC=∡DCA=((180−160)/2)=10 BAC=80−10=70 160=70+90^ AC^2 =2AD^2 −2AD^2 cos 160=2AD^2 (1+sin 70) AC=AD(√(2(1+sin 70))) =AB(√(2(1+sin 70))) (1) ΔABC AC^2 =AB^2 +BC^2 −2AB×BCcos x calcul de BC BC^2 =AB^2 +AC^2 −2AB×ACcos 70 =AB^2 +2AD^2 (1+sin 70)−2AB(AD(√(2(1+sin 70)) )cos 70 BC^2 =AB^2 +2AB^2 (1+sin 70)−2AB^2 (√(2(1+sin 70)) )cos 70 =AB^2 [3+2sin 70−2(√(2(1+sin 70)) )cos 70] ((sin x)/(AC))=((sin 70)/(BC)) ⇒((sin^2 x)/(AC^2 ))= ((sin^2 70)/(BC^2 )) ⇔((sin^2 x)/(2AB^2 (1+sin 70))) = ((sin^2 70)/(AB^2 [3+2sin 70−2(√(2(1+sin 70))) cos 70])) ((sin^2 x)/(2(1+sin 70)))=((sin^2 70)/(3+2sin 70−2(√(2(1+sin 70)) )cos 70])) =((0,88302)/(3,53218)) sin^2 x=((3,34480)/(3,53218))=0,946955 sin x=(√(0,946955)) =0,97311 x=sin^(−1) (0,97311)=76,68^°
$$\Delta\mathrm{ADC}\:\: \\ $$$$\:\:\mathrm{AD}=\mathrm{DC}\:\:\Rightarrow\measuredangle\mathrm{DAC}=\measuredangle\mathrm{DCA}=\frac{\mathrm{180}−\mathrm{160}}{\mathrm{2}}=\mathrm{10} \\ $$$$\mathrm{BAC}=\mathrm{80}−\mathrm{10}=\mathrm{70}\:\:\:\:\mathrm{160}=\mathrm{70}+\mathrm{9}\overset{} {\mathrm{0}} \\ $$$$\mathrm{AC}^{\mathrm{2}} =\mathrm{2AD}^{\mathrm{2}} −\mathrm{2AD}^{\mathrm{2}} \mathrm{cos}\:\mathrm{160}=\mathrm{2AD}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)\:\:\:\: \\ $$$$ \\ $$$$\mathrm{AC}=\mathrm{AD}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)}\:\:\:\:=\mathrm{AB}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\Delta\mathrm{ABC} \\ $$$$ \\ $$$$\mathrm{AC}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{BC}^{\mathrm{2}} −\mathrm{2AB}×\mathrm{BCcos}\:\mathrm{x} \\ $$$$\mathrm{calcul}\:\mathrm{d}{e}\:\:\:\mathrm{BC} \\ $$$$\mathrm{BC}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{AC}^{\mathrm{2}} −\mathrm{2AB}×\mathrm{ACcos}\:\mathrm{70} \\ $$$$=\mathrm{AB}^{\mathrm{2}} +\mathrm{2AD}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)−\mathrm{2AB}\left(\mathrm{AD}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right.}\:\right)\mathrm{cos}\:\mathrm{70} \\ $$$$\left.\mathrm{BC}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{2AB}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)−\mathrm{2AB}^{\mathrm{2}} \sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right.}\:\:\right)\mathrm{cos}\:\mathrm{70} \\ $$$$\left.\:=\mathrm{AB}^{\mathrm{2}} \left[\mathrm{3}+\mathrm{2sin}\:\mathrm{70}−\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right.}\:\right)\mathrm{cos}\:\mathrm{70}\right]\: \\ $$$$\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{AC}}=\frac{\mathrm{sin}\:\mathrm{70}}{\mathrm{BC}}\:\:\:\:\Rightarrow\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{AC}^{\mathrm{2}} }=\:\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{70}}{\mathrm{BC}^{\mathrm{2}} }\:\:\:\Leftrightarrow\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{2AB}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)}\:=\:\:\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{70}}{\mathrm{AB}^{\mathrm{2}} \left[\mathrm{3}+\mathrm{2sin}\:\mathrm{70}−\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)}\:\mathrm{cos}\:\mathrm{70}\right]}\:\: \\ $$$$\:\:\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}}{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right)}=\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{70}}{\left.\mathrm{3}\left.+\mathrm{2sin}\:\mathrm{70}−\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{70}\right.}\:\right)\mathrm{cos}\:\mathrm{70}\right]}\:=\frac{\mathrm{0},\mathrm{88302}}{\mathrm{3},\mathrm{53218}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}=\frac{\mathrm{3},\mathrm{34480}}{\mathrm{3},\mathrm{53218}}=\mathrm{0},\mathrm{946955} \\ $$$$\mathrm{sin}\:\mathrm{x}=\sqrt{\mathrm{0},\mathrm{946955}}\:\:=\mathrm{0},\mathrm{97311} \\ $$$$\:\:\:\:\mathrm{x}=\mathrm{sin}\:^{−\mathrm{1}} \left(\mathrm{0},\mathrm{97311}\right)=\mathrm{76},\mathrm{68}^{°} \\ $$$$ \\ $$
Commented by mr W last updated on 12/Oct/22
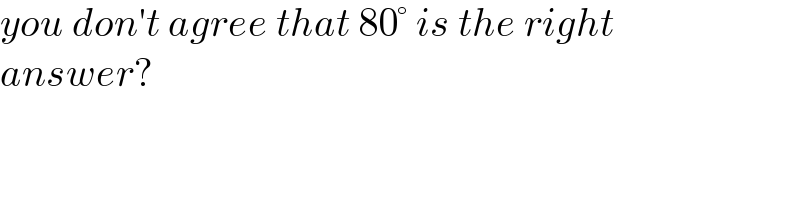
you don′t agree that 80° is the right answer?
$${you}\:{don}'{t}\:{agree}\:{that}\:\mathrm{80}°\:{is}\:{the}\:{right} \\ $$$${answer}? \\ $$
Commented by a.lgnaoui last updated on 12/Oct/22
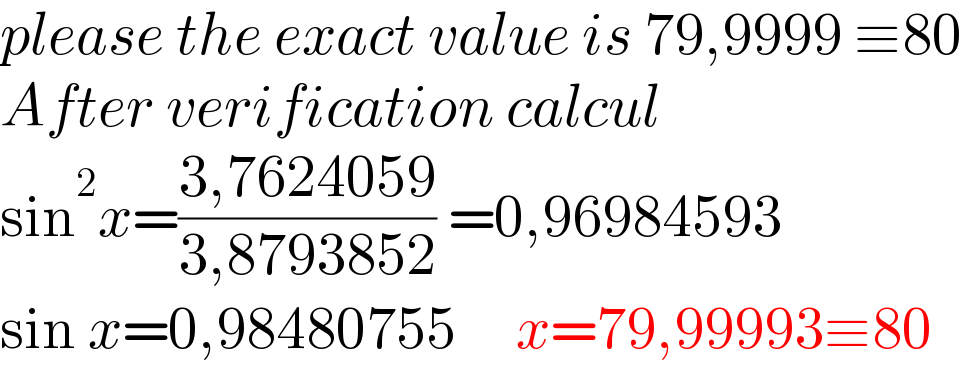
please the exact value is 79,9999 ≡80 After verification calcul sin^2 x=((3,7624059)/(3,8793852)) =0,96984593 sin x=0,98480755 x=79,99993≡80
$${please}\:{the}\:{exact}\:{value}\:{is}\:\mathrm{79},\mathrm{9999}\:\equiv\mathrm{80} \\ $$$${After}\:{verification}\:{calcul} \\ $$$$\mathrm{sin}^{\mathrm{2}} {x}=\frac{\mathrm{3},\mathrm{7624059}}{\mathrm{3},\mathrm{8793852}}\:=\mathrm{0},\mathrm{96984593} \\ $$$$\mathrm{sin}\:{x}=\mathrm{0},\mathrm{98480755}\:\:\:\:\:{x}=\mathrm{79},\mathrm{99993}\equiv\mathrm{80} \\ $$
Commented by a.lgnaoui last updated on 12/Oct/22
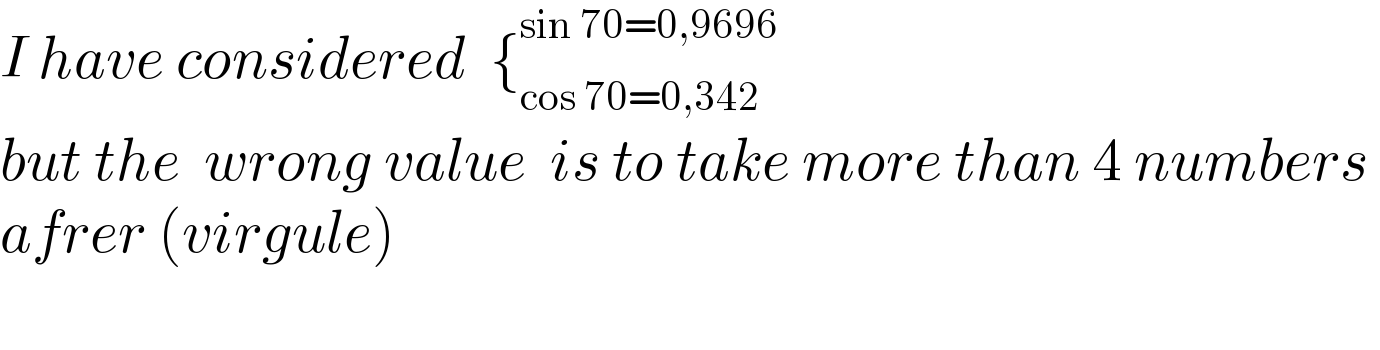
I have considered {_(cos 70=0,342) ^(sin 70=0,9696) but the wrong value is to take more than 4 numbers afrer (virgule)
$${I}\:{have}\:{considered}\:\:\left\{_{\mathrm{cos}\:\mathrm{70}=\mathrm{0},\mathrm{342}} ^{\mathrm{sin}\:\mathrm{70}=\mathrm{0},\mathrm{9696}} \right. \\ $$$${but}\:{the}\:\:{wrong}\:{value}\:\:{is}\:{to}\:{take}\:{more}\:{than}\:\mathrm{4}\:{numbers}\: \\ $$$${afrer}\:\left({virgule}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *