Question Number 177980 by infinityaction last updated on 11/Oct/22

Answered by mr W last updated on 11/Oct/22

Commented by mr W last updated on 11/Oct/22
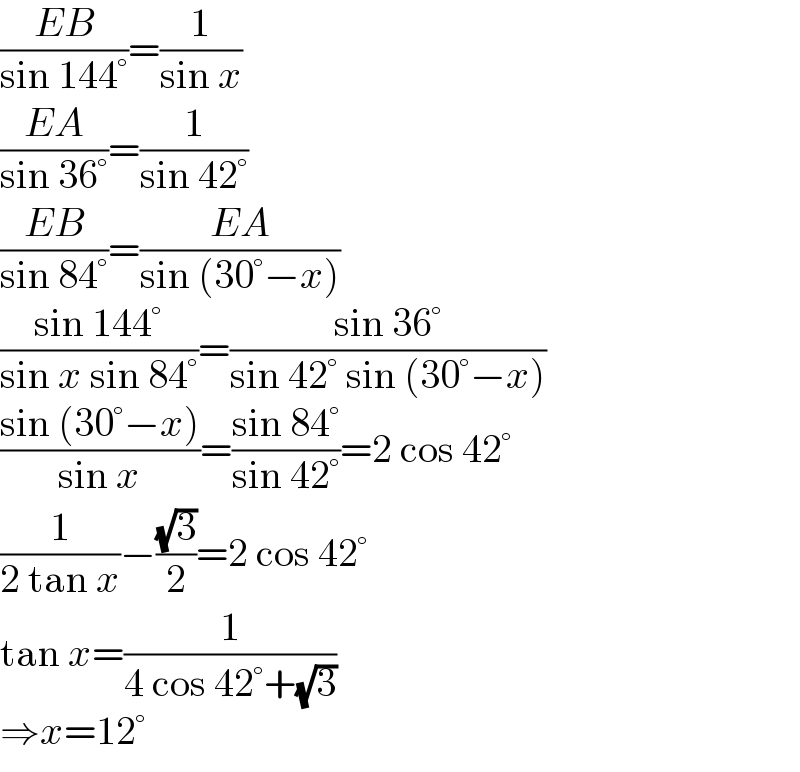
$$\frac{{EB}}{\mathrm{sin}\:\mathrm{144}°}=\frac{\mathrm{1}}{\mathrm{sin}\:{x}} \\ $$$$\frac{{EA}}{\mathrm{sin}\:\mathrm{36}°}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{42}°} \\ $$$$\frac{{EB}}{\mathrm{sin}\:\mathrm{84}°}=\frac{{EA}}{\mathrm{sin}\:\left(\mathrm{30}°−{x}\right)} \\ $$$$\frac{\mathrm{sin}\:\mathrm{144}°}{\mathrm{sin}\:{x}\:\mathrm{sin}\:\mathrm{84}°}=\frac{\mathrm{sin}\:\mathrm{36}°}{\mathrm{sin}\:\mathrm{42}°\:\mathrm{sin}\:\left(\mathrm{30}°−{x}\right)} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{30}°−{x}\right)}{\mathrm{sin}\:{x}}=\frac{\mathrm{sin}\:\mathrm{84}°}{\mathrm{sin}\:\mathrm{42}°}=\mathrm{2}\:\mathrm{cos}\:\mathrm{42}° \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:{x}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{2}\:\mathrm{cos}\:\mathrm{42}° \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{cos}\:\mathrm{42}°+\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}=\mathrm{12}° \\ $$
Commented by Tawa11 last updated on 11/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by infinityaction last updated on 12/Oct/22

$${thanks}\:{sir} \\ $$
