Question Number 178001 by Tawa11 last updated on 11/Oct/22
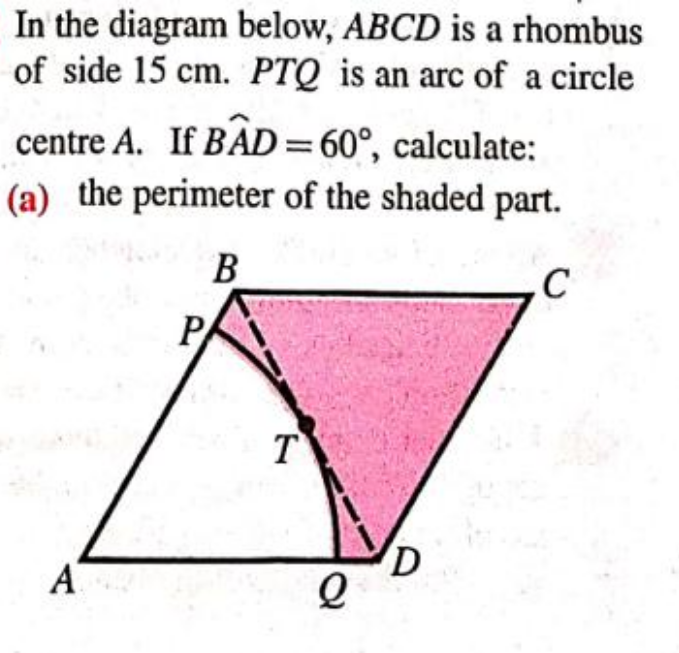
Commented by Tawa11 last updated on 11/Oct/22
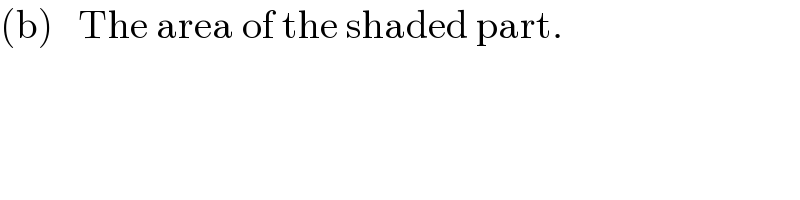
$$\left(\mathrm{b}\right)\:\:\:\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shaded}\:\mathrm{part}. \\ $$
Answered by aleks041103 last updated on 11/Oct/22
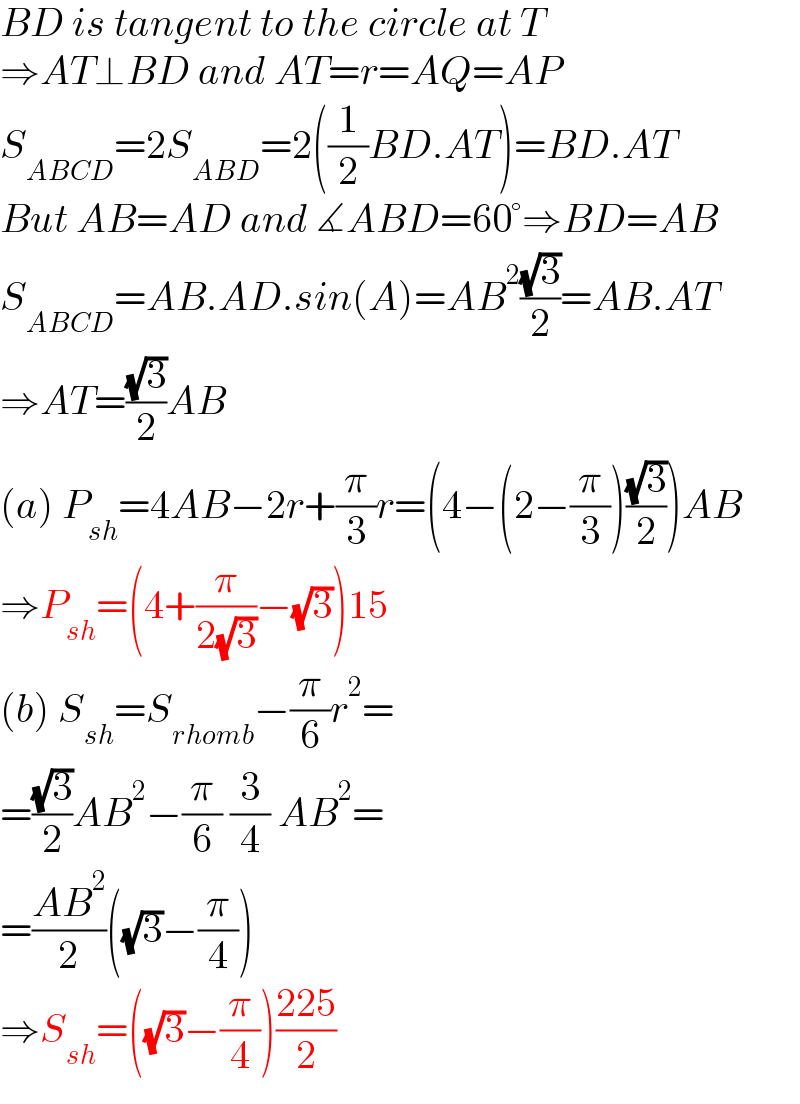
$${BD}\:{is}\:{tangent}\:{to}\:{the}\:{circle}\:{at}\:{T} \\ $$$$\Rightarrow{AT}\bot{BD}\:{and}\:{AT}={r}={AQ}={AP} \\ $$$${S}_{{ABCD}} =\mathrm{2}{S}_{{ABD}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}{BD}.{AT}\right)={BD}.{AT} \\ $$$${But}\:{AB}={AD}\:{and}\:\measuredangle{ABD}=\mathrm{60}°\Rightarrow{BD}={AB} \\ $$$${S}_{{ABCD}} ={AB}.{AD}.{sin}\left({A}\right)={AB}^{\mathrm{2}} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={AB}.{AT} \\ $$$$\Rightarrow{AT}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{AB} \\ $$$$\left({a}\right)\:{P}_{{sh}} =\mathrm{4}{AB}−\mathrm{2}{r}+\frac{\pi}{\mathrm{3}}{r}=\left(\mathrm{4}−\left(\mathrm{2}−\frac{\pi}{\mathrm{3}}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right){AB} \\ $$$$\Rightarrow{P}_{{sh}} =\left(\mathrm{4}+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−\sqrt{\mathrm{3}}\right)\mathrm{15} \\ $$$$\left({b}\right)\:{S}_{{sh}} ={S}_{{rhomb}} −\frac{\pi}{\mathrm{6}}{r}^{\mathrm{2}} = \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{AB}^{\mathrm{2}} −\frac{\pi}{\mathrm{6}}\:\frac{\mathrm{3}}{\mathrm{4}}\:{AB}^{\mathrm{2}} = \\ $$$$=\frac{{AB}^{\mathrm{2}} }{\mathrm{2}}\left(\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\Rightarrow{S}_{{sh}} =\left(\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\right)\frac{\mathrm{225}}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 12/Oct/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
