Question Number 178073 by infinityaction last updated on 12/Oct/22

Commented by Rasheed.Sindhi last updated on 12/Oct/22
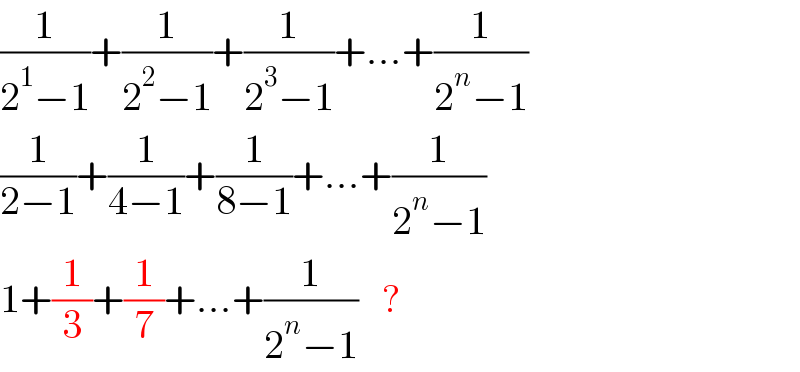
$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} −\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{8}−\mathrm{1}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}} −\mathrm{1}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{7}}+…+\frac{\mathrm{1}}{\mathrm{2}^{{n}} −\mathrm{1}}\:\:\:\:? \\ $$
Commented by mr W last updated on 12/Oct/22

$${i}\:{think}\:{it}'{s} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}^{{n}} −\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}} \\ $$
Commented by Rasheed.Sindhi last updated on 12/Oct/22
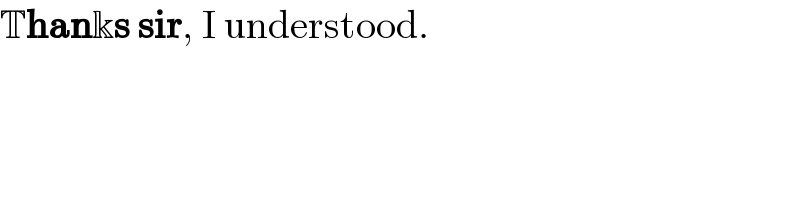
$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{sir}},\:\mathrm{I}\:\mathrm{understood}. \\ $$
Commented by infinityaction last updated on 13/Oct/22
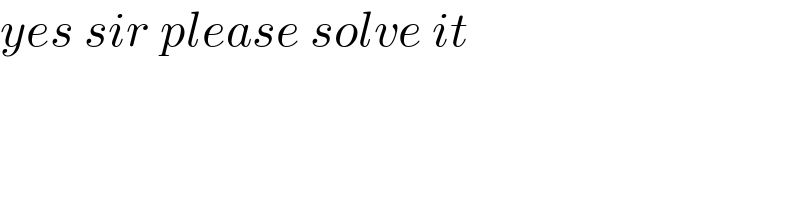
$${yes}\:{sir}\:{please}\:{solve}\:{it}\: \\ $$
Answered by mindispower last updated on 13/Oct/22
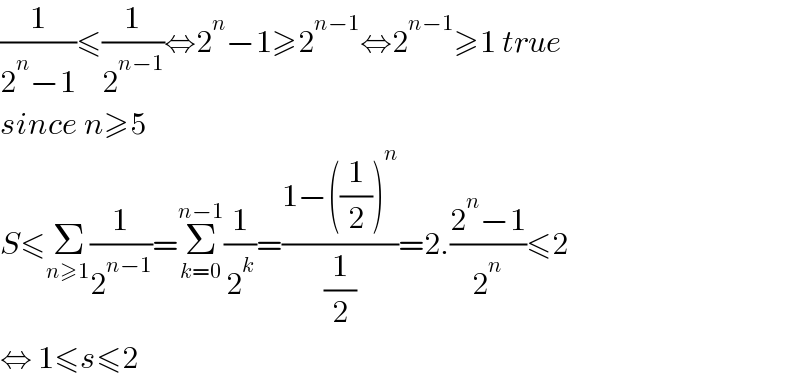
$$\frac{\mathrm{1}}{\mathrm{2}^{{n}} −\mathrm{1}}\leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\Leftrightarrow\mathrm{2}^{{n}} −\mathrm{1}\geqslant\mathrm{2}^{{n}−\mathrm{1}} \Leftrightarrow\mathrm{2}^{{n}−\mathrm{1}} \geqslant\mathrm{1}\:{true} \\ $$$${since}\:{n}\geqslant\mathrm{5} \\ $$$${S}\leqslant\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }=\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} }{\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2}.\frac{\mathrm{2}^{{n}} −\mathrm{1}}{\mathrm{2}^{{n}} }\leqslant\mathrm{2} \\ $$$$\Leftrightarrow\:\mathrm{1}\leqslant{s}\leqslant\mathrm{2} \\ $$
Commented by mindispower last updated on 13/Oct/22

$$\mathrm{2}\leqslant\frac{\mathrm{5}}{\mathrm{2}}\leqslant\frac{{n}}{\mathrm{2}} \\ $$
