Menu Close

Question-178153

Tinku Tara 0 Comments
Pin




Question Number 178153 by mnjuly1970 last updated on 13/Oct/22
Answered by mr W last updated on 13/Oct/22
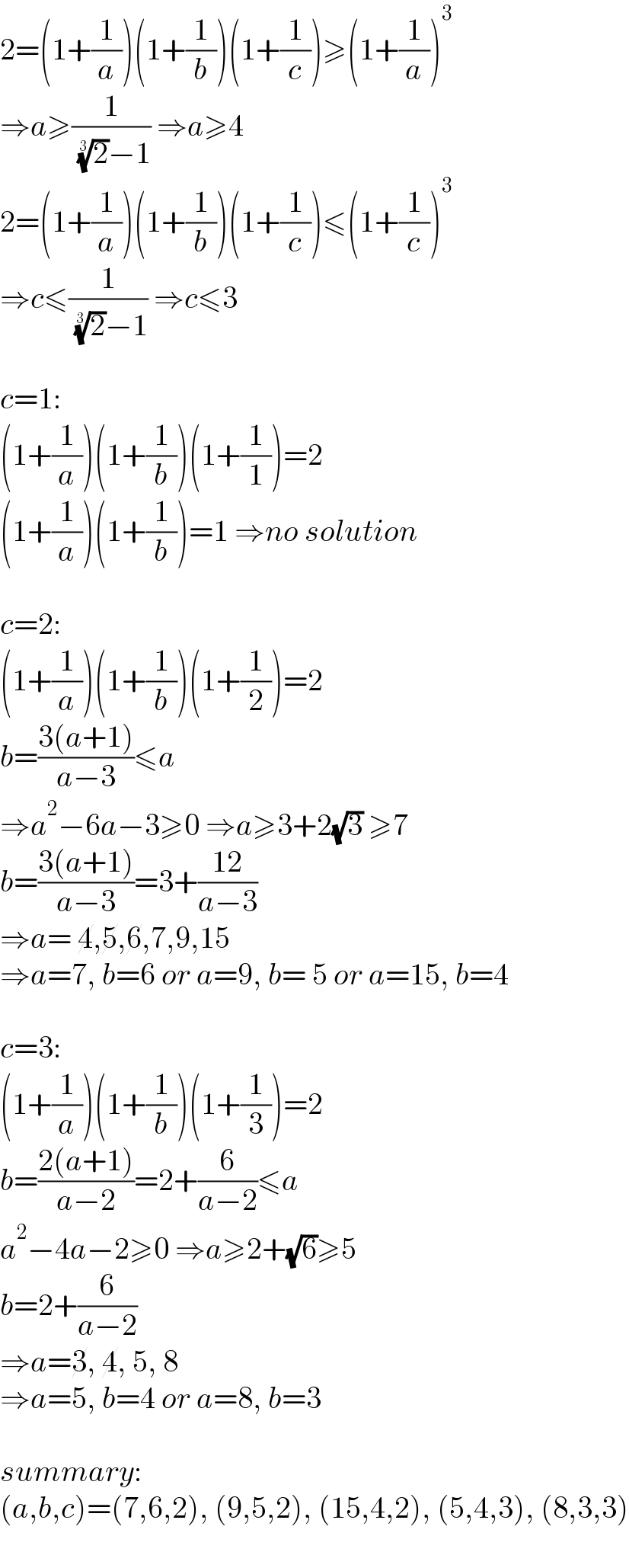
2=(1+(1/a))(1+(1/b))(1+(1/c))≥(1+(1/a))^3 ⇒a≥(1/( (2)^(1/3) −1)) ⇒a≥4 2=(1+(1/a))(1+(1/b))(1+(1/c))≤(1+(1/c))^3 ⇒c≤(1/( (2)^(1/3) −1)) ⇒c≤3 c=1: (1+(1/a))(1+(1/b))(1+(1/1))=2 (1+(1/a))(1+(1/b))=1 ⇒no solution c=2: (1+(1/a))(1+(1/b))(1+(1/2))=2 b=((3(a+1))/(a−3))≤a ⇒a^2 −6a−3≥0 ⇒a≥3+2(√3) ≥7 b=((3(a+1))/(a−3))=3+((12)/(a−3)) ⇒a= 4,5,6,7,9,15 ⇒a=7, b=6 or a=9, b= 5 or a=15, b=4 c=3: (1+(1/a))(1+(1/b))(1+(1/3))=2 b=((2(a+1))/(a−2))=2+(6/(a−2))≤a a^2 −4a−2≥0 ⇒a≥2+(√6)≥5 b=2+(6/(a−2)) ⇒a=3, 4, 5, 8 ⇒a=5, b=4 or a=8, b=3 summary: (a,b,c)=(7,6,2), (9,5,2), (15,4,2), (5,4,3), (8,3,3)
$$\mathrm{2}=\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\geqslant\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)^{\mathrm{3}} \\ $$$$\Rightarrow{a}\geqslant\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\:\Rightarrow{a}\geqslant\mathrm{4} \\ $$$$\mathrm{2}=\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\leqslant\left(\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)^{\mathrm{3}} \\ $$$$\Rightarrow{c}\leqslant\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\:\Rightarrow{c}\leqslant\mathrm{3} \\ $$$$ \\ $$$${c}=\mathrm{1}: \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}\right)=\mathrm{2} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)=\mathrm{1}\:\Rightarrow{no}\:{solution} \\ $$$$ \\ $$$${c}=\mathrm{2}: \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2} \\ $$$${b}=\frac{\mathrm{3}\left({a}+\mathrm{1}\right)}{{a}−\mathrm{3}}\leqslant{a}\: \\ $$$$\Rightarrow{a}^{\mathrm{2}} −\mathrm{6}{a}−\mathrm{3}\geqslant\mathrm{0}\:\Rightarrow{a}\geqslant\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\:\geqslant\mathrm{7} \\ $$$${b}=\frac{\mathrm{3}\left({a}+\mathrm{1}\right)}{{a}−\mathrm{3}}=\mathrm{3}+\frac{\mathrm{12}}{{a}−\mathrm{3}} \\ $$$$\Rightarrow{a}=\:\cancel{\mathrm{4}},\cancel{\mathrm{5}},\cancel{\mathrm{6}},\mathrm{7},\mathrm{9},\mathrm{15} \\ $$$$\Rightarrow{a}=\mathrm{7},\:{b}=\mathrm{6}\:{or}\:{a}=\mathrm{9},\:{b}=\:\mathrm{5}\:{or}\:{a}=\mathrm{15},\:{b}=\mathrm{4} \\ $$$$ \\ $$$${c}=\mathrm{3}: \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{2} \\ $$$${b}=\frac{\mathrm{2}\left({a}+\mathrm{1}\right)}{{a}−\mathrm{2}}=\mathrm{2}+\frac{\mathrm{6}}{{a}−\mathrm{2}}\leqslant{a} \\ $$$${a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{2}\geqslant\mathrm{0}\:\Rightarrow{a}\geqslant\mathrm{2}+\sqrt{\mathrm{6}}\geqslant\mathrm{5} \\ $$$${b}=\mathrm{2}+\frac{\mathrm{6}}{{a}−\mathrm{2}} \\ $$$$\Rightarrow{a}=\cancel{\mathrm{3}},\:\cancel{\mathrm{4}},\:\mathrm{5},\:\mathrm{8} \\ $$$$\Rightarrow{a}=\mathrm{5},\:{b}=\mathrm{4}\:{or}\:{a}=\mathrm{8},\:{b}=\mathrm{3} \\ $$$$ \\ $$$${summary}: \\ $$$$\left({a},{b},{c}\right)=\left(\mathrm{7},\mathrm{6},\mathrm{2}\right),\:\left(\mathrm{9},\mathrm{5},\mathrm{2}\right),\:\left(\mathrm{15},\mathrm{4},\mathrm{2}\right),\:\left(\mathrm{5},\mathrm{4},\mathrm{3}\right),\:\left(\mathrm{8},\mathrm{3},\mathrm{3}\right) \\ $$
Commented by mnjuly1970 last updated on 13/Oct/22
thanks alot sir W
$${thanks}\:\:{alot}\:{sir}\:{W} \\ $$
Commented by Tawa11 last updated on 13/Oct/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *