Menu Close

Question-178161

Tinku Tara 0 Comments
Pin




Question Number 178161 by mathlove last updated on 13/Oct/22
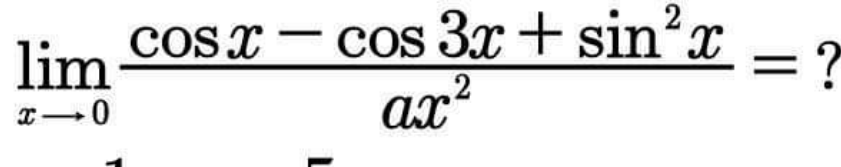
Commented by CElcedricjunior last updated on 15/Oct/22
lim_(x→0) ((cosx−cos3x+sin^2 x)/(ax^2 ))=(0/0)=FI to apply hospital lim_(x→0) ((−sinx)/(a2x))+((3sin3x)/(2ax))+((sin2x)/(2ax)) =lim_(x→0) −(1/(2a))(((sinx)/x))+(9/(2a))(((sin3x)/(3x)))+(1/a)(((sin2x)/(2x))) =−(1/(2a))+(9/(2a))+(2/(2a)) cas lim_(x→0) ((sinx)/x)=1 =((10)/(2a))=(5/a) a≠0 .......le celebre cedric junior..........
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{cosx}}−\boldsymbol{\mathrm{cos}}\mathrm{3}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{ax}}^{\mathrm{2}} }=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{\mathrm{FI}} \\ $$$$\boldsymbol{{to}}\:\boldsymbol{{apply}}\:\boldsymbol{{hospital}}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\boldsymbol{{sinx}}}{\boldsymbol{{a}}\mathrm{2}\boldsymbol{{x}}}+\frac{\mathrm{3}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}}{\mathrm{2}\boldsymbol{{ax}}}+\frac{\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{x}}}{\mathrm{2}\boldsymbol{{ax}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{a}}}\left(\frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}\right)+\frac{\mathrm{9}}{\mathrm{2}\boldsymbol{{a}}}\left(\frac{\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}}{\mathrm{3}\boldsymbol{{x}}}\right)+\frac{\mathrm{1}}{\boldsymbol{{a}}}\left(\frac{\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{x}}}{\mathrm{2}\boldsymbol{{x}}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{a}}}+\frac{\mathrm{9}}{\mathrm{2}\boldsymbol{{a}}}+\frac{\mathrm{2}}{\mathrm{2}\boldsymbol{{a}}}\:\:\boldsymbol{{cas}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}=\mathrm{1} \\ $$$$=\frac{\mathrm{10}}{\mathrm{2}\boldsymbol{{a}}}=\frac{\mathrm{5}}{\boldsymbol{{a}}}\:\:\:\:\boldsymbol{{a}}\neq\mathrm{0}\: \\ $$$$\: \\ $$$$\:…….{le}\:{celebre}\:{cedric}\:{junior}………. \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 13/Oct/22
lim_(x→0) ((cosx−cos3x+sin^2 x )/(ax^2 )) (1/a)lim_(x→0) ((−2sin((x+3x)/2)sin((x−3x)/2)+sin^2 x )/x^2 ) (1/a)lim_(x→0) ((2sin2xsinx+sin^2 x )/x^2 ) (1/a)lim_(x→0) ((2(2sinxcosx)sinx+sin^2 x )/x^2 ) (1/a)lim_(x→0) ((4sin^2 xcosx+sin^2 x )/x^2 ) (1/a)lim_(x→0) ((sin^2 x(4cosx+1) )/x^2 ) (1/a){(lim_(x→0) ((sinx )/x))^2 (lim_(x→0) (4cosx+1) ) (1/a)(1)^2 (4cos0+1)=5/a
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}{x}−\mathrm{cos3}{x}+\mathrm{sin}^{\mathrm{2}} {x}\:\:\:}{{ax}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\frac{{x}+\mathrm{3}{x}}{\mathrm{2}}\mathrm{sin}\frac{{x}−\mathrm{3}{x}}{\mathrm{2}}+\mathrm{sin}^{\mathrm{2}} {x}\:\:\:}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin2}{x}\mathrm{sin}{x}+\mathrm{sin}^{\mathrm{2}} {x}\:\:\:}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left(\mathrm{2sin}{x}\mathrm{cos}{x}\right)\mathrm{sin}{x}+\mathrm{sin}^{\mathrm{2}} {x}\:\:\:}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4sin}^{\mathrm{2}} {x}\mathrm{cos}{x}+\mathrm{sin}^{\mathrm{2}} {x}\:\:\:}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{\mathrm{2}} {x}\left(\mathrm{4cos}{x}+\mathrm{1}\right)\:\:\:}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{a}}\left\{\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}{x}\:}{{x}}\right)^{\mathrm{2}} \left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{4cos}{x}+\mathrm{1}\right)\:\right)\right. \\ $$$$\frac{\mathrm{1}}{{a}}\left(\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4cos0}+\mathrm{1}\right)=\mathrm{5}/{a}\: \\ $$
Commented by mathlove last updated on 13/Oct/22
thinks sir
$${thinks}\:{sir}\: \\ $$
Answered by cortano1 last updated on 13/Oct/22
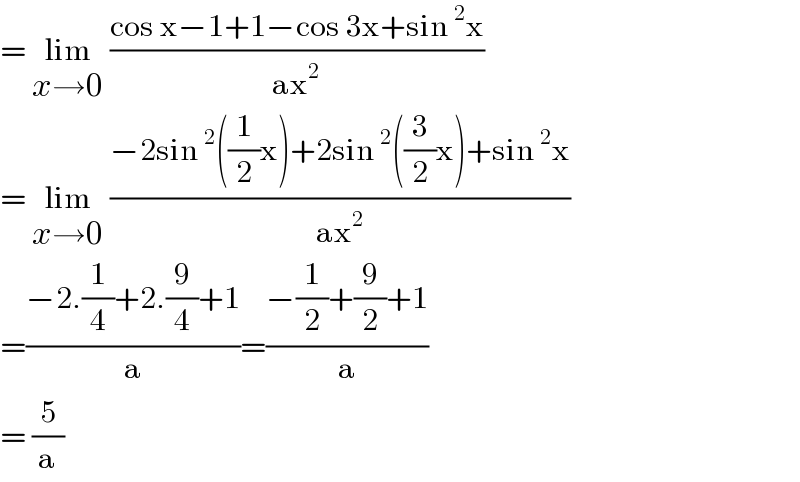
= lim_(x→0) ((cos x−1+1−cos 3x+sin^2 x)/(ax^2 )) = lim_(x→0) ((−2sin^2 ((1/2)x)+2sin^2 ((3/2)x)+sin^2 x)/(ax^2 )) =((−2.(1/4)+2.(9/4)+1)/a)=((−(1/2)+(9/2)+1)/a) = (5/a)
$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{1}+\mathrm{1}−\mathrm{cos}\:\mathrm{3x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{ax}^{\mathrm{2}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)+\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}\right)+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{ax}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}.\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}.\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{1}}{\mathrm{a}}=\frac{−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{1}}{\mathrm{a}} \\ $$$$=\:\frac{\mathrm{5}}{\mathrm{a}} \\ $$
Commented by mathlove last updated on 13/Oct/22
thanks
$${thanks} \\ $$
Answered by Acem last updated on 17/Oct/22
g(x)= cos x−cos 3x+sin^2 x = cos x−4cos^3 x+ 3cos x+ sin^2 x = 4cos x(1−cos^2 x)+ sin^2 x = sin^2 x(1+ 4cos x) lim_(x→0) f(x)= (1/a)lim_(x→0) (((sin x)/x))^2 lim_(x→0) (1+4cos x) = (5/a)
$${g}\left({x}\right)=\:\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{3}{x}+\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\:=\:\mathrm{cos}\:{x}−\mathrm{4cos}\:^{\mathrm{3}} {x}+\:\mathrm{3cos}\:{x}+\:\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\:=\:\mathrm{4cos}\:{x}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)+\:\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\:=\:\mathrm{sin}\:^{\mathrm{2}} {x}\left(\mathrm{1}+\:\mathrm{4cos}\:{x}\right) \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)=\:\frac{\mathrm{1}}{{a}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} \underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{4cos}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{5}}{{a}} \\ $$
Commented by mathlove last updated on 19/Oct/22
thanks
$${thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *