Question Number 178173 by cortano1 last updated on 13/Oct/22

Answered by Acem last updated on 13/Oct/22
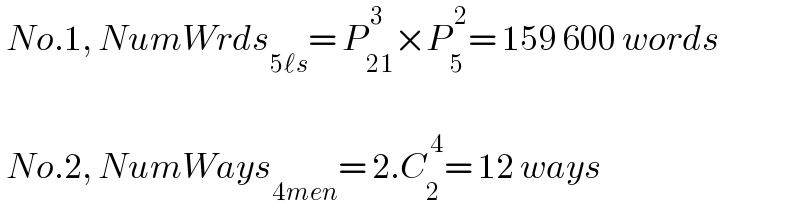
$$\:{No}.\mathrm{1},\:{NumWrds}_{\mathrm{5}\ell{s}} =\:{P}_{\mathrm{21}} ^{\:\mathrm{3}} ×{P}_{\mathrm{5}} ^{\:\mathrm{2}} =\:\mathrm{159}\:\mathrm{600}\:{words} \\ $$$$ \\ $$$$\:{No}.\mathrm{2},\:{NumWays}_{\mathrm{4}{men}} =\:\mathrm{2}.{C}_{\mathrm{2}} ^{\:\mathrm{4}} =\:\mathrm{12}\:{ways} \\ $$
Commented by mr W last updated on 14/Oct/22

$${No}.\:\mathrm{1}\:{is}\:{wrong}\:{sir}! \\ $$$${what}\:{you}\:{got}\:{is}\:{only}\:{the}\:{number}\:{of}\: \\ $$$${words}\:{in}\:{a}\:{fixed}\:{form}\:{like}\:{CCCVV}\:. \\ $$$${what}\:{about}\:{CVVCC},\:{VCVCC},\:{etc}.? \\ $$$$ \\ $$$${so}\:{correct}\:{is}:\:{we}\:{select}\:{at}\:{first}\:\mathrm{3} \\ $$$${consonants},\:{there}\:{are}\:{C}_{\mathrm{3}} ^{\mathrm{21}} \:{ways},\:{and} \\ $$$$\mathrm{2}\:{vowels},\:{there}\:{are}\:{C}_{\mathrm{2}} ^{\mathrm{5}} \:{ways}.\:{with}\:{these} \\ $$$$\mathrm{5}\:{letters}\:{we}\:{can}\:{form}\:\mathrm{5}!\:{words}. \\ $$$${therefore}\:{the}\:{answer}\:{is}\:{C}_{\mathrm{3}} ^{\mathrm{21}} ×{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{5}!\: \\ $$$${words}. \\ $$
Commented by cortano1 last updated on 14/Oct/22

$$\mathrm{yes}\:\mathrm{sir} \\ $$
Commented by Acem last updated on 14/Oct/22
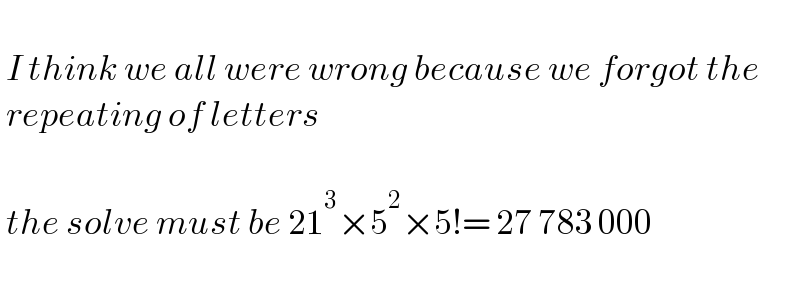
$$ \\ $$$$\:{I}\:{think}\:{we}\:{all}\:{were}\:{wrong}\:{because}\:{we}\:{forgot}\:{the} \\ $$$$\:{repeating}\:{of}\:{letters} \\ $$$$ \\ $$$$\:{the}\:{solve}\:{must}\:{be}\:\mathrm{21}^{\mathrm{3}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{5}!=\:\mathrm{27}\:\mathrm{783}\:\mathrm{000} \\ $$$$ \\ $$
Commented by mr W last updated on 14/Oct/22
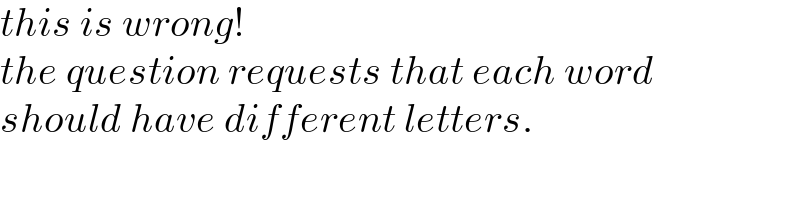
$${this}\:{is}\:{wrong}! \\ $$$${the}\:{question}\:{requests}\:{that}\:{each}\:{word}\: \\ $$$${should}\:{have}\:{different}\:{letters}. \\ $$
Commented by Acem last updated on 14/Oct/22
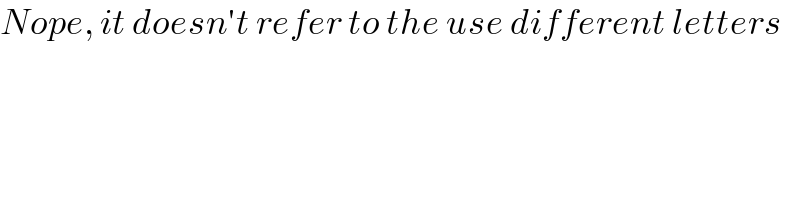
$${Nope},\:{it}\:{doesn}'{t}\:{refer}\:{to}\:{the}\:{use}\:{different}\:{letters} \\ $$
Commented by Acem last updated on 14/Oct/22
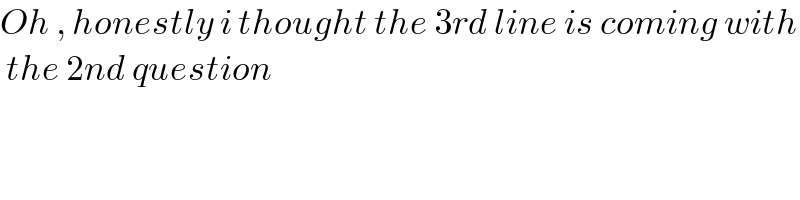
$${Oh}\:,\:{honestly}\:{i}\:{thought}\:{the}\:\mathrm{3}{rd}\:{line}\:{is}\:{coming}\:{with} \\ $$$$\:{the}\:\mathrm{2}{nd}\:{question} \\ $$
Commented by Acem last updated on 14/Oct/22
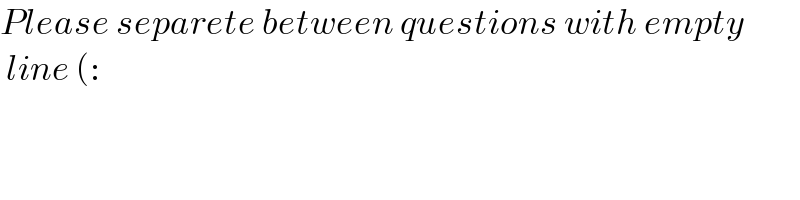
$${Please}\:{separete}\:{between}\:{questions}\:{with}\:{empty} \\ $$$$\:{line}\:\left(:\right. \\ $$
Commented by mr W last updated on 14/Oct/22
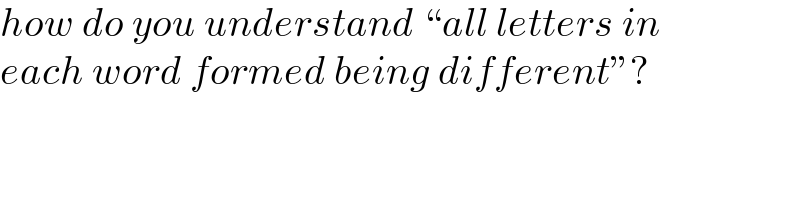
$${how}\:{do}\:{you}\:{understand}\:“{all}\:{letters}\:{in} \\ $$$${each}\:{word}\:{formed}\:{being}\:{different}''? \\ $$
Commented by Acem last updated on 14/Oct/22
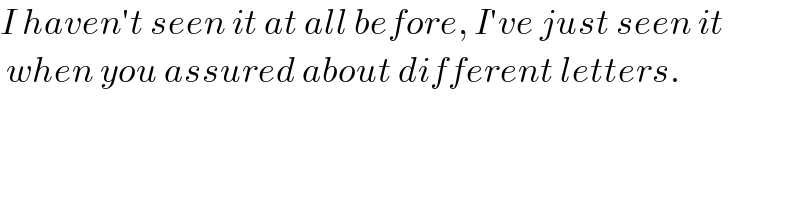
$${I}\:{haven}'{t}\:{seen}\:{it}\:{at}\:{all}\:{before},\:{I}'{ve}\:{just}\:{seen}\:{it} \\ $$$$\:{when}\:{you}\:{assured}\:{about}\:{different}\:{letters}. \\ $$
Commented by Tawa11 last updated on 14/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 13/Oct/22

$$\left(\mathrm{1}\right) \\ $$$${C}_{\mathrm{3}} ^{\mathrm{21}} ×{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{5}!=\mathrm{1596000} \\ $$$$\left(\mathrm{2}\right) \\ $$$${C}_{\mathrm{2}} ^{\mathrm{4}} ×\mathrm{2}=\mathrm{12} \\ $$
Commented by Acem last updated on 13/Oct/22
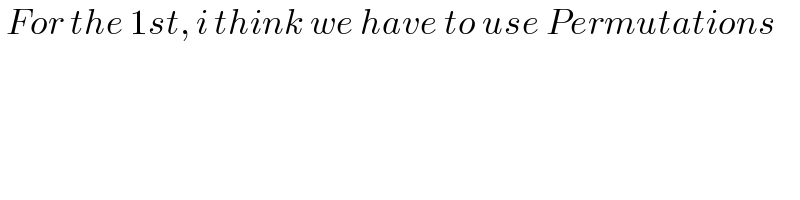
$$\:{For}\:{the}\:\mathrm{1}{st},\:{i}\:{think}\:{we}\:{have}\:{to}\:{use}\:{Permutations} \\ $$
