Question Number 178341 by haladu last updated on 15/Oct/22
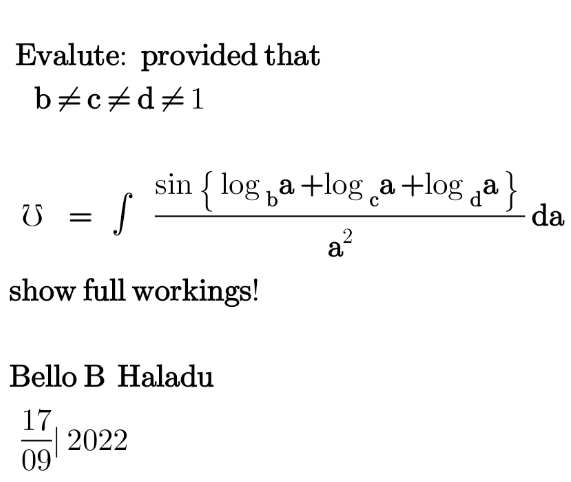
Answered by mahdipoor last updated on 15/Oct/22
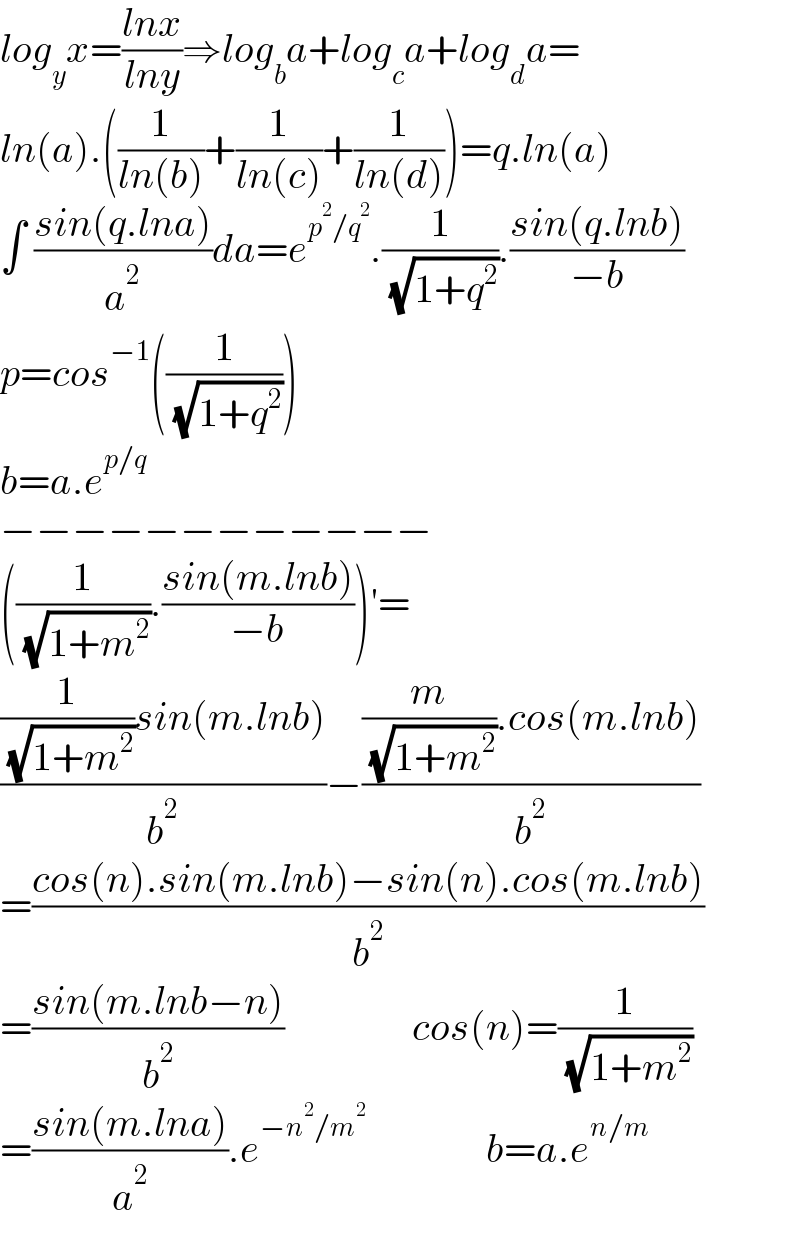
$${log}_{{y}} {x}=\frac{{lnx}}{{lny}}\Rightarrow{log}_{{b}} {a}+{log}_{{c}} {a}+{log}_{{d}} {a}= \\ $$$${ln}\left({a}\right).\left(\frac{\mathrm{1}}{{ln}\left({b}\right)}+\frac{\mathrm{1}}{{ln}\left({c}\right)}+\frac{\mathrm{1}}{{ln}\left({d}\right)}\right)={q}.{ln}\left({a}\right) \\ $$$$\int\:\frac{{sin}\left({q}.{lna}\right)}{{a}^{\mathrm{2}} }{da}={e}^{{p}^{\mathrm{2}} /{q}^{\mathrm{2}} } .\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{q}^{\mathrm{2}} }}.\frac{{sin}\left({q}.{lnb}\right)}{−{b}} \\ $$$${p}={cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{q}^{\mathrm{2}} }}\right) \\ $$$${b}={a}.{e}^{{p}/{q}} \\ $$$$−−−−−−−−−−−− \\ $$$$\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}.\frac{{sin}\left({m}.{lnb}\right)}{−{b}}\right)'= \\ $$$$\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}{sin}\left({m}.{lnb}\right)}{{b}^{\mathrm{2}} }−\frac{\frac{{m}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}.{cos}\left({m}.{lnb}\right)}{{b}^{\mathrm{2}} } \\ $$$$=\frac{{cos}\left({n}\right).{sin}\left({m}.{lnb}\right)−{sin}\left({n}\right).{cos}\left({m}.{lnb}\right)}{{b}^{\mathrm{2}} } \\ $$$$=\frac{{sin}\left({m}.{lnb}−{n}\right)}{{b}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cos}\left({n}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }} \\ $$$$=\frac{{sin}\left({m}.{lna}\right)}{{a}^{\mathrm{2}} }.{e}^{−{n}^{\mathrm{2}} /{m}^{\mathrm{2}} } \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}={a}.{e}^{{n}/{m}} \\ $$
Commented by haladu last updated on 16/Oct/22

$$\:\:\boldsymbol{\mathrm{Awasome}}\:\boldsymbol{\mathrm{Solution}}! \\ $$
